题目内容
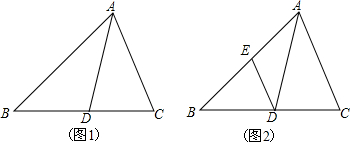
12．
如图，∠DAB=∠CAE，且AB•AD=AE•AC，请在图中找出与∠ADE相等的角，并说明理由．
分析 首先证明∠DAE=∠BAC，然后可得到△DAE∽△CAB，由相似三角形的性质即可得到答案．
解答 解：∵∠DAB=∠CAE，
∴∠DAB+∠BAE=∠CAE+∠BAE．
∴∠DAE=∠BAC．
∵AB•AD=AE•AC，
∴$\frac{AD}{AC}=\frac{AE}{AB}$．
∴△DAE∽△CAB．
∴∠ADE=∠C．
点评 本题主要考查的是相似三角形的性质和判定，掌握相似三角形的判定定理是解题的关键．
练习册系列答案
相关题目
1．已知一建筑工地仓库星期日库存水泥4t，星期一和星期二水泥的进货和出货数量如表（单位：t），请填写表中空格．
| 进出货情况 | 库存 | ||
| 星期一 | +5 | -2 | +3 |
| 星期二 | +3 | -4 | -1 |
| 合计 | +8 | -6 | +2 |