题目内容
计算:(
+
)•(
-
)(0<a<1).
| ||||
|
| ||
| 2a |
|
| 1 |
| a |
考点:二次根式的混合运算
专题:计算题
分析:先把
分母有理化和把
化简,然后合并后利用平方差公式计算,再约分即可.
| ||||
|
|
解答:解:原式=[
+
]•(
-
)
=
•
=
=-1.
| ||
| 1+a-(1-a) |
| ||
| 2a |
| ||
| a |
| 1 |
| a |
=
| ||
| a |
| ||
| a |
=
| 1-a2-1 |
| a2 |
=-1.
点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
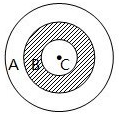 如图,有三个同心圆,由里向外的半径依次是2cm,4cm,6cm将圆盘分为三部分,飞镖可以落在A.B.C任何一部分内,则下列说法正确的是( )
如图,有三个同心圆,由里向外的半径依次是2cm,4cm,6cm将圆盘分为三部分,飞镖可以落在A.B.C任何一部分内,则下列说法正确的是( )A、飞镖在A区域可能性为
| ||
B、飞镖在B区域可能性为
| ||
C、飞镖在C区域可能性为
| ||
D、飞镖在三个区域可能性都为
|
规定以下两种变换:①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n),如g(2,1)=(-2,-1).按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(-2,3)]等于( )
| A、(-2,-3) |
| B、(2,-3) |
| C、(-2,3) |
| D、(2,3) |
以下各组式子中是同类项的是( )
| A、1和x | ||
B、-xy2和
| ||
| C、my和3y | ||
| D、a2和2a |
 实数a,b在数轴上的位置如图所示,则化简|b-a|+|a|+|b|的结果为( )
实数a,b在数轴上的位置如图所示,则化简|b-a|+|a|+|b|的结果为( )| A、2a | B、2b |
| C、2b-2a | D、0 |