题目内容
17.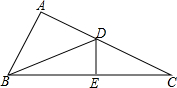 如图所示,△ADB≌△EDB,△BDE≌△CDE,点B,E,C三点在同一直线上,
如图所示,△ADB≌△EDB,△BDE≌△CDE,点B,E,C三点在同一直线上,(1)试说明:BD平分∠ABE;
(2)试说明:DE⊥BC;
(3)求∠C的度数.
分析 (1)由△ADB≌△EDB即可得到结论;
(2)由△BDE≌△CDE即可得到结论;
(3)因为三个三角形为全等三角形,则对应边相等,从而得到∠C=∠CBD=∠DBA,再利用这三角之和为90°,求得∠C的度数.
解答 (1)证明:△ADB≌△EDB,
∴∠ABD=∠EBD,
∴BD平分∠ABE;
(2)证明:∵△BDE≌△CDE,
∴∠BED=∠CED,
∵∠BED+∠CED=180°,
∴∠BED=∠CED=90°,
DE⊥BC;
(3)解:∵△ADB≌△EDB≌△EDC,
∴∠ADB=∠EDB=∠EDC,∠DEC=∠DEB∠=A,
又∵∠ADB+∠EDB+∠EDC=180°,∠DEB+∠DEC=180°
∴∠EDC=60°,∠DEC=90°,
在△DEC中,∠EDC=60°,∠DEC=90°
∴∠C=30°.
点评 主要考查了角平分线的定义,垂直定义,“全等三角形对应角相等”,发现并利用∠DEC=∠DEB∠=90°是解决本题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.
如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.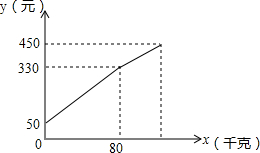 李大爷按每千克2.1元批发了一批南丰蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
李大爷按每千克2.1元批发了一批南丰蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题: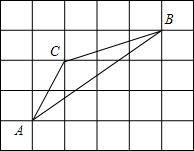 如图,在正方形网格中每个小正方形的边长均为1,△ABC的各个顶点都在正方形的顶点上,计算sinA,cosA,tanA与sinB,cosB,tanB的值.
如图,在正方形网格中每个小正方形的边长均为1,△ABC的各个顶点都在正方形的顶点上,计算sinA,cosA,tanA与sinB,cosB,tanB的值.