题目内容
11.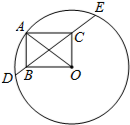 如图,⊙O的半径为20,A是⊙O上一点,以OA为对角线作矩形OBAC,且OC=12.直线BC与⊙O交于D,E两点,求CE-BD的值.
如图,⊙O的半径为20,A是⊙O上一点,以OA为对角线作矩形OBAC,且OC=12.直线BC与⊙O交于D,E两点,求CE-BD的值.
分析 过点O作OF⊥DE于点F,根据垂径定理得到DF=EF,根据余弦的定义分别求出CF、BF的长,结合图形计算即可.
解答 解:过点O作OF⊥DE于点F,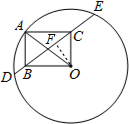
∴DF=EF,
在矩形ABOC中,OA=20,
∴BC=OA=20,
在Rt△BOC中,OC=20,
∴cos∠OCB=$\frac{OC}{BC}$=$\frac{12}{20}$=$\frac{3}{5}$,
在Rt△OCF中,cos∠OCF=$\frac{CF}{OC}$=$\frac{3}{5}$,
∴CF=$\frac{36}{5}$,
BF=BC-CF=$\frac{64}{5}$,
∴CE-BD=(EF-CF)-(DF-BF)=BF-CF=$\frac{28}{5}$.
点评 本题考查的是垂径定理的应用和矩形的性质的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
19.春节将至,某移动公司计划推出两种新的计费方式,如下表所示:
请解决以下两个问题:(通话时间为正整数)
(1)若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?
(2)对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?
| 方式1 | 方式2 | |
| 月租费 | 30元/月 | 0 |
| 本地通话费 | 0.20元/分钟 | 0.40元/分钟 |
(1)若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?
(2)对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?
20.下列说法正确的是( )
| A. | -4的平方根是±2 | B. | (-3)2的平方根是-3 | C. | 1的立方根是±1 | D. | 0的平方根是0 |
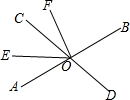 如图,直线AB与直线CD相交于点O,OE平分∠AOC,∠BOD=70°,OF⊥AB.
如图,直线AB与直线CD相交于点O,OE平分∠AOC,∠BOD=70°,OF⊥AB. 如图,平面上四个点A,B,C,D.按要求完成下列问题:
如图,平面上四个点A,B,C,D.按要求完成下列问题: 已知:如图,线段AB和射线BM交于点B.
已知:如图,线段AB和射线BM交于点B.