��Ŀ����
����Ŀ�����Ƕ��壺�����������еױ������ıȽ����ǵ��ڶ�(can)����ͼ�٣�����ABC�У�AB��AC���ǡ�B���ڶԼ���canB����ʱcanB��![]() .����֪��һ���ǵĴ�С������ǵ��ڶ�ֵ��һһ��Ӧ�ģ����������ǵ��ڶԵĶ��壬���������⣺
.����֪��һ���ǵĴ�С������ǵ��ڶ�ֵ��һһ��Ӧ�ģ����������ǵ��ڶԵĶ��壬���������⣺
(1) . can30����______ __��
(2) . ��ͼ�ڣ���֪����ABC�У�AB��AC��canB��![]() ��S��ABC��24������ABC���ܳ���
��S��ABC��24������ABC���ܳ���

���𰸡���1��![]() ����2��18
����2��18![]()
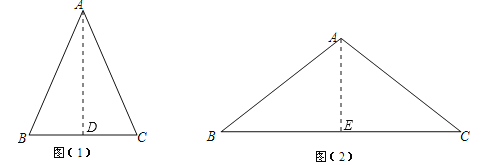
�������������������1������A��AD��BC�ڵ�D��������B=30�����ɵó�BD=![]() AB����ϵ��������ε����ʿɵó�BC=
AB����ϵ��������ε����ʿɵó�BC=![]() AB���̶��ó�canB��
AB���̶��ó�canB��
��2������A��AE��BC�ڵ�E������canB=![]() ����BC=8x��AB=5x������S��ABC=24���ɵó�x��ֵ���̶�����ܳ���
����BC=8x��AB=5x������S��ABC=24���ɵó�x��ֵ���̶�����ܳ���
����������⣺��1������A��AD��BC�ڵ�D���ߡ�B=30������cos��B=![]() =
=![]() ����BD=
����BD=![]() AB���ߡ�ABC�ǵ��������Σ���BC=2BD=
AB���ߡ�ABC�ǵ��������Σ���BC=2BD=![]() AB����can30��=
AB����can30��=![]() =
=![]() ��
��
��2������A��AE��BC�ڵ�E����canB=![]() �������BC=8x��AB=5x����AE=
�������BC=8x��AB=5x����AE=![]() =3x����S��ABC=24����
=3x����S��ABC=24����![]() BC��AE=12x2=24����ã�x=
BC��AE=12x2=24����ã�x=![]() ����AB=AC=
����AB=AC=![]() ��BC=
��BC=![]() ���Ӷ��ɵ���ABC���ܳ�Ϊ
���Ӷ��ɵ���ABC���ܳ�Ϊ![]() ��
��

��ϰ��ϵ�д�
 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
�����Ŀ