题目内容
17. 正方形ABCD的边长为a,以相邻的两边为直径分别画两个半圆,求阴影部分的面积.
正方形ABCD的边长为a,以相邻的两边为直径分别画两个半圆,求阴影部分的面积.
分析 先判断出两半圆交点为正方形的中心,连接OB,则可得出所产生的四个小弓形的面积相等,继而根据阴影部分的面积可得出答案.
解答 解:易知:两半圆的交点即为正方形的中心,设此点为O,连接AC,则AC必过点O,连接OB;
则图中的四个小弓形的面积相等,
∴两个半圆的面积-Rt△ABC的面积=4个小弓形的面积,
∴两个小弓形的面积为($\frac{π{a}^{2}}{8}-\frac{{a}^{2}}{4}$),
图中阴影部分的面积=正方形面积-[Rt△ADC-2个小弓形的面积]=a2-[$\frac{1}{2}{a}^{2}$-($\frac{π{a}^{2}}{8}-\frac{{a}^{2}}{4}$)].
点评 此题考查了扇形的面积计算,解答本题的关键是得出两半圆的交点是正方形的中心,求出小弓形的面积,有一定难度,注意仔细观察图形.

练习册系列答案
相关题目
8. 如图,如果直线l是△ABC的对称轴,其中∠B=70°,那么∠BAC的度数等于( )
如图,如果直线l是△ABC的对称轴,其中∠B=70°,那么∠BAC的度数等于( )
 如图,如果直线l是△ABC的对称轴,其中∠B=70°,那么∠BAC的度数等于( )
如图,如果直线l是△ABC的对称轴,其中∠B=70°,那么∠BAC的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
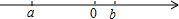 有理数a、b在数轴上如图,
有理数a、b在数轴上如图, 已知二次函数y=-x2+2x+3.
已知二次函数y=-x2+2x+3. 如图,AB为⊙O的直径,OC⊥AB,P为OA上任意一点,PH⊥BC于H,交OC于D.求证:OP=OD.
如图,AB为⊙O的直径,OC⊥AB,P为OA上任意一点,PH⊥BC于H,交OC于D.求证:OP=OD. 在所给的数轴上表示下列五个数,并把这五个数按从小到大的顺序,用“<”号连接起来.
在所给的数轴上表示下列五个数,并把这五个数按从小到大的顺序,用“<”号连接起来.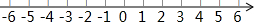 在数轴上表示下列各数,并按从大到小的顺序排列,用“>”连接起来:
在数轴上表示下列各数,并按从大到小的顺序排列,用“>”连接起来: