Question

△ABC内接于⊙O，BC是⊙O的直径．
（1）过点B的切线与OA的延长线交于点P，如图甲，若∠C=∠ABC，AB=2，求切线BP的长；
（2）过点A作AD⊥BC于D，交⊙O于H，过点B作弦BF交AD于E，交⊙O于F，且AE=BE，如图乙．求证：=．

Answer 1

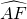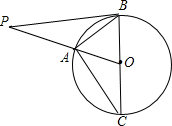（1）解：∵BC是直径，
∴∠BAC=90°．
∵∠C=∠ABC，
∴∠ABC=60°，∠C=30°．
又OA=OB，
∴△AOB是等边三角形，
∴BO=AB=2，∠AOB=60°
∵BP是⊙O的切线，
∴∠PBO=90°．
在Rt△PBO中，PB=BO•tan∠POB=2•tan60°=；

（2）证明：∵AD⊥BC，BC是直径，
∴=．
∵AE=BE，∴∠ABF=∠BAH，
∴=，
∴=．
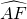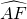分析：（1）根据BC是直径，可得∠BAC=90°，在Rt△ABC中，∠C=∠ABC，可推出∠ABC=60°，∠C=30°，而OA=OB，可知△AOB是等边三角形，故∠AOB=60°，OB=AB=2，又根据BP是⊙O的切线，得∠PBO=90°，在Rt△PBO中，解直角三角形可求BP；
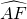（2）所对的圆周角为∠AHB，所对的圆周角为∠ABF，由垂径定理可知=，则∠AHB=∠BAH，又由AE=EB可知∠BAH=∠ABF，可得∠AHB=∠ABF．
点评：本题考查了垂径定理、圆周角定理、切线的性质．关键是将证明弧相等的问题转化为证明所对的圆周角相等．