题目内容
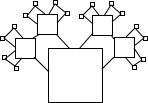 一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是
一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是| 109 |
| 64 |
| 109 |
| 64 |
分析:解答本题只需求出第二次和第三次以及第四次所得正方形的边长进而求出其面积和原正方形的面积相加即可.
解答:解:由于第一个正方形的边长为1,则第二、第三、第四个正方形的边长为
、
、
,
∴第二次新生成图形的面积为:
×
×
×2=
,
第三次新生成图形的面积为:
×
×
×4=
,
∵由题可得生长到第4次所得缺角正方形的边长为:
,
又∵缺角三角形的中心在先前正方形的角上,
∴它少了
的面积,即剩
,
所以一个缺角三角形的面积是 (
)2×
=
,
总共的面积=
×8=
,
则生长到第4次后,所得图形的面积是=1+
+
+
=1
.
故答案为:
.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
∴第二次新生成图形的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
第三次新生成图形的面积为:
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
∵由题可得生长到第4次所得缺角正方形的边长为:
| 1 |
| 8 |
又∵缺角三角形的中心在先前正方形的角上,
∴它少了
| 1 |
| 4 |
| 3 |
| 4 |
所以一个缺角三角形的面积是 (
| 1 |
| 8 |
| 3 |
| 4 |
| 3 |
| 256 |
总共的面积=
| 3 |
| 256 |
| 3 |
| 32 |
则生长到第4次后,所得图形的面积是=1+
| 3 |
| 8 |
| 3 |
| 16 |
| 3 |
| 32 |
| 23 |
| 32 |
故答案为:
| 109 |
| 64 |
点评:此题考查了图形的变化.通过计算找出图形变化的规律,利用规律推出正方形的面积是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
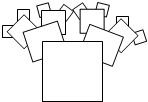 一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图所示)若第一个正方形的边长是1,则生长到第4次所得缺角正方形的面积是
一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图所示)若第一个正方形的边长是1,则生长到第4次所得缺角正方形的面积是 的正方形.如图所示,由左图至右图,利用面积的不同表示方法写出一个代数恒等式是( )
的正方形.如图所示,由左图至右图,利用面积的不同表示方法写出一个代数恒等式是( )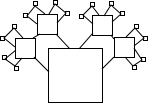 一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是________.
一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是________.