题目内容
AB是⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=4cm,BD=9cm,则CD= cm,BC= cm.
考点:垂径定理,勾股定理
专题:计算题
分析:如图,连接OC,先计算出AB=13cm,则半径OA=OB=6.5cm,所以OD=OA-AD=2.5cm,再在Rt△OCD中,利用勾股定理计算出CD=6cm,然后在Rt△CDB中,利用勾股定理计算出BC.
解答:解: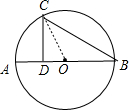 如图,连接OC,
如图,连接OC,
∵AD=4cm,BD=9cm,
∴AB=13cm,
∴OA=OB=6.5cm,
∴OD=OA-AD=2.5cm,
∵CD⊥AB,
∴∠CDB=90°,
在Rt△OCD中,CD=
=
=6(cm),
在Rt△CDB中,BC=
=
=3
(cm).
故答案为6,3
.
 如图,连接OC,
如图,连接OC,∵AD=4cm,BD=9cm,
∴AB=13cm,
∴OA=OB=6.5cm,
∴OD=OA-AD=2.5cm,
∵CD⊥AB,
∴∠CDB=90°,
在Rt△OCD中,CD=
| OC2-OD2 |
| 6.52-2.52 |
在Rt△CDB中,BC=
| CD2+BD2 |
| 62+(2.5+6.5)2 |
| 13 |
故答案为6,3
| 13 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 如图,笔直的公路的旁有三个便民店A、B、C,现测得A、B两个便民店之间的距离为2km,B、C两个便民店之间的距离为1km;一个公路的路标恰好在A、C两个便民店的正中间点O处,则路标与B店之间的距离为
如图,笔直的公路的旁有三个便民店A、B、C,现测得A、B两个便民店之间的距离为2km,B、C两个便民店之间的距离为1km;一个公路的路标恰好在A、C两个便民店的正中间点O处,则路标与B店之间的距离为 如图,在△ABC中,∠C=90°,AM是∠CAB的平分线,CM=20cm,那么M到AB的距离为
如图,在△ABC中,∠C=90°,AM是∠CAB的平分线,CM=20cm,那么M到AB的距离为