题目内容
20022﹣20012+20002﹣19992+19982﹣…+22﹣12．
2005003
解析试题分析：首先利用平方差公式分解各式，可得（2002+2001）（2002﹣2001）+（2000+1999）（2000﹣1999）+…（2+1）（2﹣1），然后再求1到2002的和即可．
解：原式=（2002+2001）（2002﹣2001）+（2000+1999）（2000﹣1999）+…（2+1）（2﹣1）
=2002+2001+2000+1999+1998+…+2+1
=
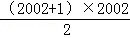
=2005003．
考点：平方差公式
点评：此题考查了平方差公式分解因式的应用．此题难度适中，注意观察、分析，得到规律是解此题的关键．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
设m=2002+2001×2002+2001×20022+…+2001×20022000，n=20022001．则正确的关系是（ ）
| A、m=n×2001 | B、m=n | C、m=n÷2002 | D、m=n+2002 |