题目内容
15.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值3,则实数m的值为( )| A. | $\frac{3}{2}$或-$\sqrt{2}$ | B. | $\sqrt{2}$或-$\sqrt{2}$ | C. | 2或-$\sqrt{2}$ | D. | $\frac{3}{2}$或-$\frac{3}{2}$ |
分析 求出二次函数对称轴为直线x=m,再分m<-2,-2≤m≤1,m>1三种情况,根据二次函数的增减性列方程求解即可.
解答 解:二次函数y=-(x-m)2+m2+1,
可化为:y=-x2+2mx+1,
故二次函数的对称轴为直线x=m,
①m<-2时,x=-2时二次函数有最大值,
此时-(-2-m)2+m2+1=3,
解得m=-$\frac{3}{2}$,与m<-2矛盾,故m值不存在;
②当-2≤m≤1时,x=m时,二次函数有最大值,
此时,m2+1=3,
解得m=-$\sqrt{2}$,m=$\sqrt{2}$(舍去);
③当m>1时,x=1时二次函数有最大值,
此时,-(1-m)2+m2+1=3,
解得m=$\frac{3}{2}$.
综上所述,m的值为$\frac{3}{2}$或-$\sqrt{2}$.
故选:A.
点评 本题考查了二次函数的最值问题,难点在于分情况讨论.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
7.下列计算正确的是( )
| A. | a3•a2=a6 | B. | x2+x2=x4 | C. | (-2a2b)3=-6a6b3 | D. | 2-2=$\frac{1}{4}$ |
4.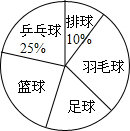 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
解答下列问题:
(1)a=30,b=24;
(2)试估计上述500名学生中最喜欢羽毛球运动的人数;
(3)该学校将组织趣味运动会,九(1)班决定从3名喜欢乒乓球、1名喜欢羽毛球,1名喜欢篮球的5名学生中随机抽取2人作为班级代表参加活动,那么被抽到的2名同学都是喜欢乒乓球的概率是多少?请用树状图或列表法说明理由.
 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:| 球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
| 人数 | a | 12 | 36 | 18 | b |
(1)a=30,b=24;
(2)试估计上述500名学生中最喜欢羽毛球运动的人数;
(3)该学校将组织趣味运动会,九(1)班决定从3名喜欢乒乓球、1名喜欢羽毛球,1名喜欢篮球的5名学生中随机抽取2人作为班级代表参加活动,那么被抽到的2名同学都是喜欢乒乓球的概率是多少?请用树状图或列表法说明理由.
5.64的平方根是( )
| A. | ±8 | B. | ±4 | C. | 8 | D. | 32 |
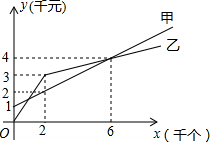 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,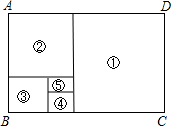 如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④
如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④
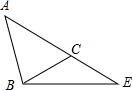 如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.
如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.