题目内容
15. 如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.(1)求证:CP为⊙O的切线;
(2)BP=1,CP=$\sqrt{5}$.
①求⊙O的半径;
②若M为AC上一动点,则OM+DM的最小值为$\frac{2}{3}$$\sqrt{14}$.
分析 (1)连接OC,根据已知证得∠POC=∠PCD,由∠POC+∠OCD=90°.证得∠PCD+∠OCD=90°,即∠OCP=90°,即可证得CP为⊙O的切线;
(2)①设⊙O的半径为r.在Rt△OCP中,利用勾股定理即可求得;
②先证得△COP∽△DOC,根据相似三角形对应边成比例求得CD的长,作点O点关于AC的对称点E,连接ED,交AC于M,此时OM+DM=ED的最小,连接AE,EC,证得四边形AOCE是菱形,进而证得EC=2,∠ECD=90°,然后根据勾股定理即可求得ED,即OM+DM的最小值.
解答  (1)证明:连接OC,如图1,
(1)证明:连接OC,如图1,
∵∠PCD=2∠BAC,∠POC=2∠BAC,
∴∠POC=∠PCD,
∵CD⊥AB于点D,
∴∠ODC=90°.
∴∠POC+∠OCD=90°.
∴∠PCD+∠OCD=90°.
∴∠OCP=90°.
∴半径OC⊥CP.
∴CP为⊙O的切线.
(2)解:①设⊙O的半径为r.
在Rt△OCP中,OC2+CP2=OP2,
∵BP=1,CP=$\sqrt{5}$.
∴r2+($\sqrt{5}$)2=(r+1)2,
解得r=2.
∴⊙O的半径为2.
②∵∠OCP=∠ODC=90°,∠COD=∠POC,
∴△COP∽△DOC,
∴$\frac{CP}{OP}$=$\frac{CD}{OC}$,即$\frac{\sqrt{5}}{3}$=$\frac{CD}{2}$,
∴CD=$\frac{2}{3}$$\sqrt{5}$,
如图2,作点O点关于AC的对称点E,连接AE,EC,此时OM+DM=ED, ∵AC垂直平分OE,
∵AC垂直平分OE,
∴AE=AO,
∴∠OAC=∠EAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠EAC=∠OCA,
∴AE∥OC,
∵OA=AE=OC=2,
∴四边形AOCE是菱形,
∴EC=2,∠ECD=90°,
在RT△ECD中,EC=2,CD=$\frac{2}{3}$$\sqrt{5}$,
∴ED=$\sqrt{C{E}^{2}+C{D}^{2}}$=$\frac{2}{3}$$\sqrt{14}$.
∵OM+DM的最小值为$\frac{2}{3}$$\sqrt{14}$.
故答案为$\frac{2}{3}$$\sqrt{14}$.
点评 本题考查了切线的判定定理,轴对称的性质,菱形的判定和性质,勾股定理的应用,熟练掌握性质定理是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,可以看作是由一个等腰直角三角形旋转若干次生成的,则每次旋转的度数是( )
如图,可以看作是由一个等腰直角三角形旋转若干次生成的,则每次旋转的度数是( )| A. | 45° | B. | 50° | C. | 60° | D. | 72° |
| A. | y1>y2>y3 | B. | y3>y2>y1 | C. | y2>y1>y3 | D. | y3>y1>y2 |
 如图,下列语句正确的是( )
如图,下列语句正确的是( )| A. | 直线AC和BD是不同的直线 | B. | 直线AD=AB+BC+CD | ||
| C. | 射线DC和DB不是同一条射线 | D. | 射线AB和BD不是同一条射线 |
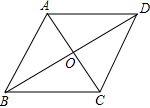 如图,菱形ABCD中,AC、BD交于点O,若AC=4,BD=6,则菱形的面积为12.
如图,菱形ABCD中,AC、BD交于点O,若AC=4,BD=6,则菱形的面积为12. 如图,抛物线y=(x+1)2+k与x轴交于A,B两点,与y轴交于点C(0,-3),抛物线的对称轴上存在一点P,使得PB+PC的值最小,求此时点P的坐标.
如图,抛物线y=(x+1)2+k与x轴交于A,B两点,与y轴交于点C(0,-3),抛物线的对称轴上存在一点P,使得PB+PC的值最小,求此时点P的坐标.