题目内容
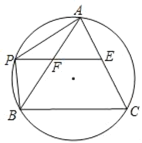
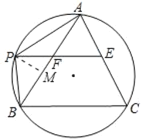
【题目】如图,等边三角形ABC中,E、F为AC、AB中点,EF延长线交△ABC外接圆于P,则PB:AP的数值为_____(提示:圆内接四边形对角互补)
【答案】![]()
【解析】
根据△ABC是等边三角形,E、F为AC、AB中点,证得EF=AF=BF,设AF=BF=x,利用△APB∽△AFP,求得PB=![]() PF;作PM⊥AB于M,再设FM=y,通过计算得PF=2y,PM=
PF;作PM⊥AB于M,再设FM=y,通过计算得PF=2y,PM=![]() y,PB=2
y,PB=2![]() y,BM=x﹣y,根据勾股定理得y=
y,BM=x﹣y,根据勾股定理得y=![]() x,继而求得答案.
x,继而求得答案.
∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∵∠APB+∠ACB=180°,
∴∠APB=120°,
∵E、F为AC、AB中点,
∴EF∥BC,EF=![]() BC=
BC=![]() AB=AF=BF,
AB=AF=BF,
∴∠AFE=∠ABC=60°,
∴∠AFP=120°=∠APB,
∵∠PAB=∠FAP,
∴△APB∽△AFP,
∴![]() ,
,
∴AP2=AF×AB,
设AF=BF=x,则AB=2x,
∴AP2=2x2,AP=![]() x,
x,
∴![]() ,
,
∴PB=![]() PF,
PF,
作PM⊥AB于M,如图所示:
∵∠PFM=∠AFE=60°,
∴∠FPM=30°,
∴FM=![]() PF,PM=
PF,PM=![]() FM,
FM,
设FM=y,则PF=2y,PM=![]() y,PB=2
y,PB=2![]() y,BM=x﹣y,
y,BM=x﹣y,
在![]() 中,由勾股定理得:(
中,由勾股定理得:(![]() y)2+(x﹣y)2=(2
y)2+(x﹣y)2=(2![]() y)2,
y)2,
解得:y=![]() x(负值舍去),
x(负值舍去),
∴y=![]() x,
x,
∴PB=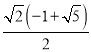 x,
x,
∴![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目