Question

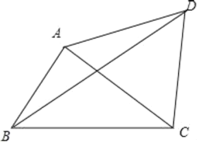
【题目】如图，在△ABC中，以AC为边向外作等边△ACD．

（1）画出将△ABD绕点A顺时针旋转60°后得到的△ACE；

（2）若∠ABC＝60°，AB＝3，BC＝5，求BD的长．

Answer 1

【答案】（1）见解析；（2）7

【解析】

（1）根据旋转变换的定义和性质作图可得；
（2）连接BE，过点E作EF⊥BC，交CB延长线于点F，先证△ABE为等边三角形得AB=AE=BE=3，∠ABE=60°，由∠ABC=60°知∠EBF=60°，据此知BF=BEcos60°=，EF=BEsin60°=，根据勾股定理可得EC=7，再证△EAC≌△BAD得BD=CE=7．

解：（1）如图所示，△ACE即为所求．

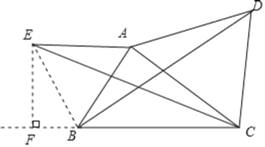
（2）如图，连接BE，过点E作EF⊥BC，交CB延长线于点F，

∵∠BAE＝∠CAD＝60°，AE＝AB，

∴△ABE是等边三角形，

∴AB＝AE＝BE＝3，∠ABE＝60°，

∵∠ABC＝60°，

∴∠EBF＝60°，

∴BF＝BEcos60°＝，EF＝BEsin60°＝，

则EC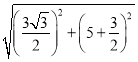＝＝＝7，

∵△ACD是等边三角形，

∴AC＝AD，∠CAD＝60°，

∴∠EAC＝∠BAD，

∴△EAC≌△BAD（SAS），

∴BD＝CE＝7．