题目内容
 已知:AB是直径,CD是∠ACB的角平分线,AC=8,BC=6.
已知:AB是直径,CD是∠ACB的角平分线,AC=8,BC=6.(1)求证:AC•BC=CG•CD;
(2)求AB、AD、BD的长.
考点:圆周角定理,勾股定理,相似三角形的判定与性质
专题:
分析:(1)由条件可证明△ACG∽△DCB,可得
=
,即AC•BC=CG•CD;
(2)由勾股定理可求得AB=10,由∠ACD=∠BCD,可得AD=BD,在Rt△ABD中由勾股定理可得出AD和BD的长.
| AC |
| CD |
| CG |
| BC |
(2)由勾股定理可求得AB=10,由∠ACD=∠BCD,可得AD=BD,在Rt△ABD中由勾股定理可得出AD和BD的长.
解答:(1)证明:∵CD平分∠ACB,
∴∠ACD=∠BCD,且∠CAG=∠CDB(同弧所对的圆周角),
∴△ACG∽△DCB,
∴
=
,即AC•BC=CG•CD;
(2)解:∵AB为直径,
∴∠ACB=∠ADB=90°,
∵∠ACD=∠DCB,
∴AD=BD,
在Rt△ABC中,AC=8,BC=6,可求得AB=10,
在Rt△ABD中,由勾股定理可求得AD=BD=5
.
∴∠ACD=∠BCD,且∠CAG=∠CDB(同弧所对的圆周角),
∴△ACG∽△DCB,
∴
| AC |
| CD |
| CG |
| BC |
(2)解:∵AB为直径,
∴∠ACB=∠ADB=90°,
∵∠ACD=∠DCB,
∴AD=BD,
在Rt△ABC中,AC=8,BC=6,可求得AB=10,
在Rt△ABD中,由勾股定理可求得AD=BD=5
| 2 |
点评:本题主要考查圆周角定理及相似三角形的判定和性质,在第(1)问是证明△ACG∽△DCB、在第(2)问中得到AD=BD是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,直线y=kx(k>0)与双曲线y=
如图,直线y=kx(k>0)与双曲线y=| 4 |
| x |
| A、28 | B、20 | C、36 | D、-20 |
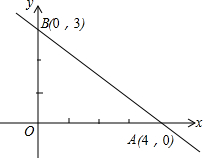 如图,直线y=-
如图,直线y=-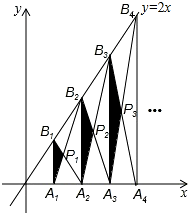 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )