题目内容
 如图,AB是⊙O的直径,过B点作弦BC,OD⊥BC,垂足为E,若BC=8cm,∠ABC=30°,则DE的长为
如图,AB是⊙O的直径,过B点作弦BC,OD⊥BC,垂足为E,若BC=8cm,∠ABC=30°,则DE的长为
- A.2

- B.4

- C.
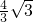
- D.

C
分析:如图,连接AC.根据圆周角定理、三角形中位线定理求得OE= AC;然后由图形知ED=OD-OE.
AC;然后由图形知ED=OD-OE.
解答: 解:如图,连接AC.
解:如图,连接AC.
∵AB是⊙O的直径(已知),
∴∠C=90°(直径所对的圆周角是直角),
∵OD⊥BC(已知),
∴∠BEO=∠C=90°,
∴OD∥AC(同位角相等,两直线平行),
点O是线段AB的中点,
∴OE是△ABC的中位线,
∴OE= AC.
AC.
∵在直角△ABC中,BC=8cm,∠ABC=30°,
∴AC=BC•tan∠ABC=8× =
= (cm),AC=
(cm),AC= AB=OA=OD,
AB=OA=OD,
∴ED=OD-OE=AC-OE= AC=
AC= (cm).
(cm).
故选C.
点评:此题考查了圆周角定理、三角形中位线的性质、以及平行线的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.
分析:如图,连接AC.根据圆周角定理、三角形中位线定理求得OE=
 AC;然后由图形知ED=OD-OE.
AC;然后由图形知ED=OD-OE.解答:
 解:如图,连接AC.
解:如图,连接AC.∵AB是⊙O的直径(已知),
∴∠C=90°(直径所对的圆周角是直角),
∵OD⊥BC(已知),
∴∠BEO=∠C=90°,
∴OD∥AC(同位角相等,两直线平行),
点O是线段AB的中点,
∴OE是△ABC的中位线,
∴OE=
 AC.
AC.∵在直角△ABC中,BC=8cm,∠ABC=30°,
∴AC=BC•tan∠ABC=8×
 =
= (cm),AC=
(cm),AC= AB=OA=OD,
AB=OA=OD,∴ED=OD-OE=AC-OE=
 AC=
AC= (cm).
(cm).故选C.
点评:此题考查了圆周角定理、三角形中位线的性质、以及平行线的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为