题目内容
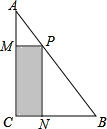 如图,将直角三角形余料截出一个矩形PMCN,∠C=90°,AC=40cm,BC=30cm,点P、M、N分别在AB、AC、BC上,设CN=x.
如图,将直角三角形余料截出一个矩形PMCN,∠C=90°,AC=40cm,BC=30cm,点P、M、N分别在AB、AC、BC上,设CN=x.(1)试用含x的代数式表示PN;
(2)设矩形PMCN的面积为y(cm2),当x为何值时,y的值最大?最大值是多少?
考点:相似三角形的应用,二次函数的最值
专题:
分析:(1)由PN∥AC,可得△BPN∽△BAC,根据相似三角形的性质可得
=
,进而得到用含x的代数式表示PN的式子;
(2)根据矩形PMCN的面积=PN•CN得出y与x的二次函数关系式,再根据二次函数的性质即可求解.
| PN |
| AC |
| BN |
| BC |
(2)根据矩形PMCN的面积=PN•CN得出y与x的二次函数关系式,再根据二次函数的性质即可求解.
解答:解:(1)∵将直角三角形余料截出一个矩形PMCN,∠C=90°,点P、M、N分别在AB、AC、BC上,
∴PN∥AC,
∴△BPN∽△BAC,
∴
=
,即
=
,
∴PN=
;
(2)∵矩形PMCN的面积=PN•CN=
•x=-
x2+40x,
∴y=-
x2+40x=-
(x-15)2+300,
∴当x=15cm时,y的值最大,最大值是300cm2.
∴PN∥AC,
∴△BPN∽△BAC,
∴
| PN |
| AC |
| BN |
| BC |
| PN |
| 40 |
| 30-x |
| 30 |
∴PN=
| 4(30-x) |
| 3 |
(2)∵矩形PMCN的面积=PN•CN=
| 4(30-x) |
| 3 |
| 4 |
| 3 |
∴y=-
| 4 |
| 3 |
| 4 |
| 3 |
∴当x=15cm时,y的值最大,最大值是300cm2.
点评:本题考查了相似三角形的应用,其中涉及到相似三角形的判定与性质,矩形的面积公式,二次函数的最值的确定.根据相似三角形对应边成比例得到用含x的代数式表示PN的式子是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
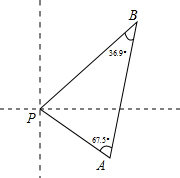 我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈
我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈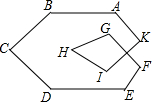 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为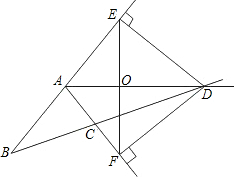 如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连结EF.
如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连结EF. 如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.
如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.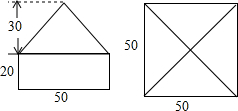 如图是一个尖顶石柱的三视图(单位:厘米).如果每立方米的石料重2.4t,求这个尖顶石柱的质量.
如图是一个尖顶石柱的三视图(单位:厘米).如果每立方米的石料重2.4t,求这个尖顶石柱的质量. 如图,将直角三角形ABC沿射线BC的方向平移得到△DEF,求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到△DEF,求图中阴影部分的面积.