题目内容
9.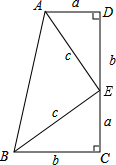 如图,在梯形ABCD中,∠C=∠D=90°.利用面积法证明勾股定理.
如图,在梯形ABCD中,∠C=∠D=90°.利用面积法证明勾股定理.
分析 先利用“边角边”证明△ADE和△EBC全等,根据全等三角形对应角相等可得∠AED=∠CBE,再求出∠AEB=90°,然后根据梯形的面积公式和梯形的面积等于三个直角三角形的面积列出方程整理即可得证.
解答 证明:在△ADE和△EBC中,
$\left\{\begin{array}{l}{AD=EC}\\{∠C=∠D=90°}\\{DE=BC}\end{array}\right.$,
∴△ADE≌△EBC(SAS),
∴∠AED=∠CBE,
∵∠CBE+∠BEC=90°,
∴∠AED+∠BEC=90°,
∴∠AEB=90°,
∴梯形的面积=$\frac{1}{2}$(a+b)(a+b)=2×$\frac{1}{2}$ab+$\frac{1}{2}$c2,
整理得,a2+b2=c2.
点评 本题考查了勾股定理的证明,全等三角形的判定与性质,求出∠AEB=90°是解题的关键,难点在于利用梯形的面积列出方程.

练习册系列答案
相关题目
19.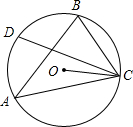 如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
 如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )| A. | $\frac{β-α}{2}$ | B. | $\frac{α-β}{3}$ | C. | $\frac{β+α}{3}$ | D. | $\frac{β+α}{4}$ |
20. 已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
 已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )| A. | a<0 | B. | b<c | C. | b>a | D. | c>0 |
4.若7x3y3与一个多项式的积是28x7y3-21x5y5+2y•(7x3y3)2,则这个多项式为( )
| A. | 4x4-3x2y2+14x3y4 | B. | 4x2y-3x2y2 | ||
| C. | 4x4-3y2 | D. | 4x4-3xy2+7xy3 |
1.已知点P(a,a+3)在抛物线y=x2-7x+19图象上,则点P关于原点O的对称点P′的坐标是( )
| A. | (4,7) | B. | (-4,-7) | C. | (4,-7) | D. | (-4,7) |
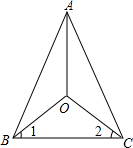 已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,求证:
已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,求证: