题目内容
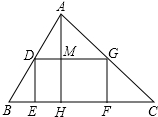 如图一块三角形土地的底边BC=100m,高线AH=80m,现要沿着底边BC修建一座底面是矩形DEFG的大楼,设矩形DEFG的一边长DE=x(m).
如图一块三角形土地的底边BC=100m,高线AH=80m,现要沿着底边BC修建一座底面是矩形DEFG的大楼,设矩形DEFG的一边长DE=x(m).(1)矩形DEFG的另一边长DG是多少(用关于x的代数式表示);
(2)试用关于x代数式表示大楼底面矩形DEFG的面积S;
(3)当DE为多少时,大楼底面的面积最大?最大值是多少?
考点:相似三角形的应用,二次函数的应用
专题:应用题
分析:(1)DE=x,则MH=x,AM=AH-MH=80-x,证明△ADG∽△ABC,利用相似比可求出DG的长;
(2)根据矩形的面积公式易得S=-
x2+100x(0<x<80);
(3)利用二次函数的最值问题求解.
(2)根据矩形的面积公式易得S=-
| 5 |
| 4 |
(3)利用二次函数的最值问题求解.
解答:解:(1)DE=x,则MH=x,AM=AH-MH=80-x,
∵DG∥BC,
∴△ADG∽△ABC,
∴
=
,即
=
,
∴DG=(-
x+100)m;
(2)S=DE•DG
=x(-
x+100)
=-
x2+100x(0<x<80);
(3)y=-
x2+100x
当x=-
=40时,S最大值=
=2000,
即DE为40m时,大楼底面的面积最大,最大值是2000m2.
∵DG∥BC,
∴△ADG∽△ABC,
∴
| DG |
| BC |
| AM |
| AH |
| DG |
| 100 |
| 80-x |
| 80 |
∴DG=(-
| 5 |
| 4 |
(2)S=DE•DG
=x(-
| 5 |
| 4 |
=-
| 5 |
| 4 |
(3)y=-
| 5 |
| 4 |
当x=-
| 100 | ||
2×(-
|
| 0-1002 | ||
4×(-
|
即DE为40m时,大楼底面的面积最大,最大值是2000m2.
点评:本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.也考查了二次函数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
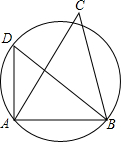 已知在相对灯塔A、B的张角为56°的弓形海域内有一暗礁群,如图,某海监执法大队正在对灯塔A,B的张角为55°的C处巡航维权,试问是否会有触礁的危险.
已知在相对灯塔A、B的张角为56°的弓形海域内有一暗礁群,如图,某海监执法大队正在对灯塔A,B的张角为55°的C处巡航维权,试问是否会有触礁的危险. 把m棵树分别栽在如图所示的甲乙两块地上(阴影部分),求甲乙两块地中的每棵树平均所占面积的比.
把m棵树分别栽在如图所示的甲乙两块地上(阴影部分),求甲乙两块地中的每棵树平均所占面积的比. 同学们都知道五月的第二个星期天是“母亲节”,小聪和妈妈一起去商场购物,他们发现商场现在举行促销打折活动(信息如图所示),小聪和妈妈给奶奶买了300元的营养品,让小聪结账.小聪在收银台旁发现有妈妈最喜欢的百合花,价格是2.5元钱一枝,他最多能买几枝又不需要多花钱呢?
同学们都知道五月的第二个星期天是“母亲节”,小聪和妈妈一起去商场购物,他们发现商场现在举行促销打折活动(信息如图所示),小聪和妈妈给奶奶买了300元的营养品,让小聪结账.小聪在收银台旁发现有妈妈最喜欢的百合花,价格是2.5元钱一枝,他最多能买几枝又不需要多花钱呢?