题目内容
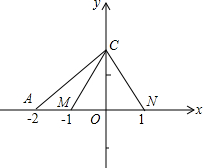 如图,在直角坐标系中,△CMN是等边三角形,且OM=ON=1,OA=2,P是x轴正半轴上的任意一点,当P点在x轴正半轴上移动时,是否存在这样的一点P,使△CMA∽△CNP?若存在,请确定P点的位置并画出△CNP,并给予证明;若不存在,请说明理由.
如图,在直角坐标系中,△CMN是等边三角形,且OM=ON=1,OA=2,P是x轴正半轴上的任意一点,当P点在x轴正半轴上移动时,是否存在这样的一点P,使△CMA∽△CNP?若存在,请确定P点的位置并画出△CNP,并给予证明;若不存在,请说明理由.考点:相似三角形的判定,等边三角形的性质
专题:常规题型
分析:根据等边三角形的性质得∠CMN=∠CNM=60°,CM=CN=2OM=2,则∠CMA=∠CNP=120°,根据两组对应边的比相等且夹角对应相等的两个三角形相似,当
=
时,△CMA∽△CNP,即
=
,解得NP=1,然后计算出OP的长,从而可确定P点坐标.
| CM |
| CN |
| MA |
| NP |
| 2 |
| 2 |
| 1 |
| NP |
解答:解:∴△CMN是等边三角形,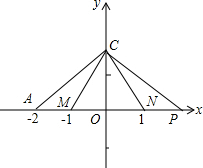
∴∠CMN=∠CNM=60°,
∵OM=ON=1,
∴CM=CN=2OM=2,
∴∠CMA=∠CNP=120°,
∴当
=
时,△CMA∽△CNP,即
=
,解得NP=1,
∴OP=ON+NP=2,
∴P点坐标为(2,0),如图.

∴∠CMN=∠CNM=60°,
∵OM=ON=1,
∴CM=CN=2OM=2,
∴∠CMA=∠CNP=120°,
∴当
| CM |
| CN |
| MA |
| NP |
| 2 |
| 2 |
| 1 |
| NP |
∴OP=ON+NP=2,
∴P点坐标为(2,0),如图.
点评:本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了等边三角形的性质.

练习册系列答案
相关题目
在平面直角坐标系中,点(-4,5)关于原点对称的点的坐标为( )
| A、(4,-5) |
| B、(4,5) |
| C、(-4,-5) |
| D、(-4,5) |
使二次根式
有意义的x的取值范围是( )
| 4-2x |
| A、x≥4 | B、x≥2 |
| C、x≤2 | D、x≤4 |
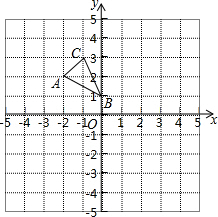 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1). 如图,已知∠1=∠B,∠BAD=∠BCD,请指出图中所有的平行直线,并说明理由.
如图,已知∠1=∠B,∠BAD=∠BCD,请指出图中所有的平行直线,并说明理由. 如图,在数a,b,c,d,e中,若x>3,那么x可取的数为:
如图,在数a,b,c,d,e中,若x>3,那么x可取的数为: 在如图所示的方格纸中,每一个正方形的面积为1,按要求画图,并回答问题.
在如图所示的方格纸中,每一个正方形的面积为1,按要求画图,并回答问题.