题目内容
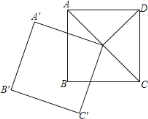
【题目】如图，正方形ABCD的面积为8cm2，且其对角线相交于点O，点O是正方形A′B′C′O的一个顶点，如果两个正方形的边长相等，那么正方形A′B′C′O绕点O无论怎样转动，两个正方形重叠部分的面积为_____cm2．
【答案】2
【解析】
求两个正方形重叠部分的面积，首先应证明△AOE≌△BOF，从而将求重叠部分的面积转化为△AOB的面积．
解：如图，AB与A′O交于点E，BC与OC′交于点F，连接BO，
∵ABCD和A′B′C′O都是边长相等的正方形，
∴OA＝OB，∠AOB＝∠A′OC′＝90°，∠BAO＝∠OBC＝45°，
∴∠AOB∠BO A′＝∠A′OC′∠BO A′，即∠AO A′＝∠BOF，
∴△AOE≌△BOF，
∴重叠部分面积为：S△BOE＋S△BOF＝S△BOE＋S△AOE＝
S正方形ABCD＝×8＝2cm2．
故答案为2．
练习册系列答案
相关题目
【题目】某商店销售一种商品，通过记录，发现该商品从开始销售至销售的第x天结束时（x为整数）的总销量y（件）满足二次函数关系，销量情况记录如下表：
x | 0 | 1 | 2 | 3 |
y | 0 | 58 | 112 | 162 |
（1）求y与x之间的函数关系式（不需要写自变量的取值范围）；
（2）求：销售到第几天结束时，该商品全部售完？
（3）若第m天的销量为22件，求m的值．
