题目内容
如图,直线b由直线a: 沿x轴向右平移9个单位得到,则直线a与直线b的距离为 .
沿x轴向右平移9个单位得到,则直线a与直线b的距离为 .
【答案】分析:直线a、b分别与x轴交于A、B,过B点作BC⊥直线a,CD⊥AB于D点,先确定A点坐标为(-3,0),根据平移确定B点坐标为(6,0),设C点坐标为(m,n),则n= m+4,易得△ADC∽△CDB,则CD:DB=AD:DB,即CD2=AD•DB,于是(
m+4,易得△ADC∽△CDB,则CD:DB=AD:DB,即CD2=AD•DB,于是( m+4)2=(m+3)(6-m),解得m1=
m+4)2=(m+3)(6-m),解得m1= ,m2=-3(舍去),然后计算出BD与CD的值,再利用勾股定理计算BC即可.;
,m2=-3(舍去),然后计算出BD与CD的值,再利用勾股定理计算BC即可.;
解答:解: 直线a、b分别与x轴交于A、B,过B点作BC⊥直线a,CD⊥AB于D点,如图,
直线a、b分别与x轴交于A、B,过B点作BC⊥直线a,CD⊥AB于D点,如图,
把x=0代入y= x+4得
x+4得 x+4=0,解得x=-3,则A点坐标为(-3,0),
x+4=0,解得x=-3,则A点坐标为(-3,0),
∵直线b由直线a: 沿x轴向右平移9个单位得到,
沿x轴向右平移9个单位得到,
∴B点坐标为(6,0),
设C点坐标为(m,n),则n= m+4,
m+4,
∵△ADC∽△CDB,
∴CD:DB=AD:DB,即CD2=AD•DB,
∴( m+4)2=(m+3)(6-m),解得m1=
m+4)2=(m+3)(6-m),解得m1= ,m2=-3(舍去),
,m2=-3(舍去),
∴BD=6- =
= ,CD=
,CD= ×
× +4=
+4= ,
,
∴BC= =
= .
.
故答案为 .
.
点评:本题考查了一次函数图象与几何变换:一次函数y=kx+b(k、b为常数,k≠0)的图象为直线,当直线平移时k不变,当向上平移m个单位,则平移后直线的解析式为y=kx+b+m.也考查了勾股定理与三角形相似得判定与性质.
 m+4,易得△ADC∽△CDB,则CD:DB=AD:DB,即CD2=AD•DB,于是(
m+4,易得△ADC∽△CDB,则CD:DB=AD:DB,即CD2=AD•DB,于是( m+4)2=(m+3)(6-m),解得m1=
m+4)2=(m+3)(6-m),解得m1= ,m2=-3(舍去),然后计算出BD与CD的值,再利用勾股定理计算BC即可.;
,m2=-3(舍去),然后计算出BD与CD的值,再利用勾股定理计算BC即可.;解答:解:
 直线a、b分别与x轴交于A、B,过B点作BC⊥直线a,CD⊥AB于D点,如图,
直线a、b分别与x轴交于A、B,过B点作BC⊥直线a,CD⊥AB于D点,如图,把x=0代入y=
 x+4得
x+4得 x+4=0,解得x=-3,则A点坐标为(-3,0),
x+4=0,解得x=-3,则A点坐标为(-3,0),∵直线b由直线a:
 沿x轴向右平移9个单位得到,
沿x轴向右平移9个单位得到,∴B点坐标为(6,0),
设C点坐标为(m,n),则n=
 m+4,
m+4,∵△ADC∽△CDB,
∴CD:DB=AD:DB,即CD2=AD•DB,
∴(
 m+4)2=(m+3)(6-m),解得m1=
m+4)2=(m+3)(6-m),解得m1= ,m2=-3(舍去),
,m2=-3(舍去),∴BD=6-
 =
= ,CD=
,CD= ×
× +4=
+4= ,
,∴BC=
 =
= .
.故答案为
 .
.点评:本题考查了一次函数图象与几何变换:一次函数y=kx+b(k、b为常数,k≠0)的图象为直线,当直线平移时k不变,当向上平移m个单位,则平移后直线的解析式为y=kx+b+m.也考查了勾股定理与三角形相似得判定与性质.

练习册系列答案
相关题目
 如图,直线b由直线a:
如图,直线b由直线a: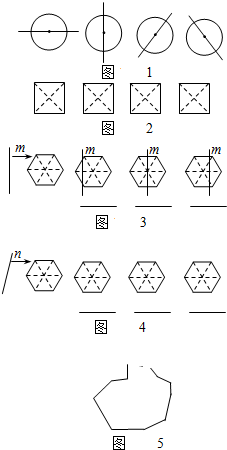 (2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).
(2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1). (2012•荆州模拟)如图,直线L1交直线L2于y轴上一点A(0,6),交x轴上另一点C.l2交x轴于另一点B,二次函数y=ax2-6ax-16a (a>0)的图象过B、C两点,点P是线段OC上由O向C移动的动点,线段OP=t(1<t<8)
(2012•荆州模拟)如图,直线L1交直线L2于y轴上一点A(0,6),交x轴上另一点C.l2交x轴于另一点B,二次函数y=ax2-6ax-16a (a>0)的图象过B、C两点,点P是线段OC上由O向C移动的动点,线段OP=t(1<t<8)