Question

如图1，在△ABC中，AC=BC，∠ACB=90°，点D为AB边中点，以点D为顶点作∠PDQ=90°，DP、DQ分别交直线AC、BC于E、F，分别过E、F作AB的垂线，垂足分别为M、N．
（1）求证：EM+FN=

2

2

AC；
（2）把∠PDQ绕点D旋转，当点E在线段AC的延长线上时（如图2），则线段EM、FN、AC之间满足的关系式是

 

；
（3）在∠PDQ绕点D由图1到图2的旋转的过程中，设DP交直线BC于点G，连接BE，若FG=10，AE=3CE，求BE的长．

Answer 1

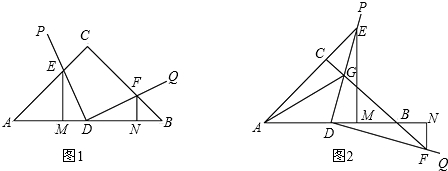
分析：（1）连接CD，由D为等腰直角三角形斜边AB的中点，根据三线合一得到CD垂直于AB，CD为角平分线，从而得到∠ECD=∠B=45°，根据斜边上的中线等于斜边的一半得到CD=DB，再由∠EDC与∠CDF互余，且∠CDF与∠FDB互余，根据同角的余角相等得到∠EDC=∠FDB，根据ASA可得三角形CED与三角形FBD全等，根据全等三角形的对应边相等可得ED=FD，再根据同角的余角相等得到一对角相等，一对直角相等，且DE=DF，根据AAS得到三角形EDM与三角形FND全等，可得MD=FN，又三角形AEM为等腰直角三角形，故EM=AM，所以EM+FN等量代换为AD，而在等腰直角三角形ACD中，根据45°的余弦函数定义可得AD=

2

2

AC，从而得证；
（2）连接CD，同理可得EM-FN=

2

2

AC；
（3）过D作DH垂直于AC，又BC垂直于AC，得到DH与BC平行，根据D为AB中点，得到H也为AC中点，得到DH为三角形ABC的中位线，根据中位线的性质得到DH等于BC的一半，即为AC的一半，又AE=3EC，得到AC=2EC，从而得到BC=2EC，可得HD=EC，设CE=x，则AE=3x，AC=AE-CE=2x，可得AH=HC=CE=x，且AC=BC=EH=2EC=2x，由∠HAD=45°，∠AHD=90°，得到△AHD为等腰直角三角形，同理△AEM和△FND都为等腰直角三角形，可表示出AM=EM=

2

2

AE=

3 2

2

x，进而得到HD=AH=x，由EC=CH=x，
得到C为HE的中点，即CG为中位线，根据三角形中位线定理得到CG=

1

2

HD=

1

2

x，用GB=BC-CG，表示出GB，由第二问得到EM-FN=

2

2

AC，将表示出的EM及AC代入表示出FN，即为DN，利用勾股定理表示出BF，由GF=GB+BF，将GF=10代入，列出关于x的方程，求出方程的解得到x的值，进而确定出EM及BM的长，在直角三角形BEM中，由EM及BM的长，利用勾股定理即可求出EB的值．

解答：（1）证明：连接CD，
∵AC=BC，∠ACB=90°，点D为AB边中点，
∴∠ACD=∠DCB=

1

2

∠ACB=45°，CD⊥AB，
又∠A=∠B=45°，
∴∠ECD=∠FBD，
又D为Rt△ABC斜边AB的中点，
∴CD=BD=

1

2

AB，
∵∠PDQ=90°，
∴∠EDC+∠CDF=90°，
又CD⊥AB，∴∠CDF+∠FDB=90°，
∴∠EDC=∠FDB，
在△CED和△FBD中，

∠EDC=∠FBD CD=BD ∠EDC=∠FDB

，
∴△CED≌△FBD（ASA），
∴ED=FD，
又∵∠MED+∠EDM=90°，∠EDM+∠FDN=90°，
∴∠MED=∠NDF，
在△EDM和△DFN中，

∠MED=∠NDF ∠EMD=∠DNF=90° ED=FD

，
∴△EDM≌△DFN（AAS），
∴MD=FN，
又∠A=45°，∠EMA=90°，
∴∠AEM=∠A=45°，
∴AM=EM，
∴EM+FN=AM+MD=AD，
在Rt△ACD中，cosA=cos45°=

AD

AC

=

2

2

，即AD=

2

2

AC，
∴EM+FN=

2

2

AC；

（2）连接CD，
∵AC=BC，∠ACB=90°，点D为AB边中点，
∴∠ACD=∠DCB=45°，CD⊥AB，
又∠A=∠ABC=45°，
∴∠ECD=∠FBD=135°，
又D为Rt△ABC斜边AB的中点，
∴CD=BD=

1

2

AB，
∵∠PDQ=90°，
∴∠FDB+∠EDN=90°，
又CD⊥AB，∴∠EDC+∠EDN=90°，
∴∠EDC=∠FDB，
在△CED和△FBD中，

∠ECD=∠FBD CD=BD ∠EDC=∠FDB

，
∴△CED≌△FBD（ASA），
∴ED=FD，
又∵∠MED+∠EDM=90°，∠EDM+∠FDN=90°，
∴∠MED=∠NDF，
在△EDM和△DFN中，

∠MED=∠NDF ∠EMD=∠DNF=90° ED=FD

，
∴△EDM≌△DFN（AAS），
∴MD=FN，
又∠A=45°，∠EMA=90°，
∴∠AEM=∠EAM=45°，
∴AM=EM，
∴EM-FN=AM-MD=AD，
在Rt△ACD中，cosA=cos45°=

AD

AC

=

2

2

，即AD=

2

2

AC，
∴EM-FN=

2

2

AC；

（3）根据题意画出图形，如图所示：
连接BE，过D作DH⊥AC，又BC⊥AC，且D为AB的中点，
∴H为AC的中点，即DH为△ABC的中位线，
∴DH∥BC，且DH=

1

2

BC=

1

2

AC，
由AE=3EC，设EC=x，则AE=3x，AC=AE-CE=2x，
∴AH=HC=CE=x，且AC=BC=EH=2EC=2x，
又∠HAD=45°，∠AHD=90°，
∴△AHD为等腰直角三角形，
同理△AEM和△FNB都为等腰直角三角形，
∴AM=EM=

2

2

AE=

3 2

2

x，
∴HD=AH=x，
∵EC=CH=x，
∴C为HE的中点，又CG∥HD，
∴G为ED的中点，即CG为三角形EHD的中位线，
∴CG=

1

2

HD=

1

2

x，
∴GB=BC-CG=2x-

1

2

x=

3

2

x，
由第二问得到EM-FN=

2

2

AC，
∴

3 2

2

x-FN=

2

x，即FN=DN=

2

2

x，
∴BF=x，又GF=10，
∴GF=GB+BF=

3

2

x+x=10，解得：x=4，
∴EM=

3 2

2

x=6

2

，BM=AB-AM=2

2

x-

3 2

2

x=2

2

，
在直角三角形BEM中，根据勾股定理得：EB=

EM2+BM2

=4

5

．
故答案为：EM-FN=

2

2

AC

点评：此题考查了等腰直角三角形的性质，全等三角形的判定与性质，锐角三角函数定义，三角形的中位线定理，要求学生借助图形，多次利用转化的思想，寻找全等所需的条件，由三角形的全等来解决问题，第二问是探究结论型题，需要充分抓住已知条件或图形的特征，找准问题的突破口，由浅入深，多角度，多侧面探寻联系符合题设的有关知识，合理组合，发现新结论，本题应参照第一问的证明方法来探究第二问的结论，第三问作出辅助线DH，构造三个全等三角形是解题的关键．