Question

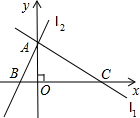
（2012•荆州模拟）如图，直线L₁交直线L₂于y轴上一点A（0，6），交x轴上另一点C．l₂交x轴于另一点B，二次函数y=ax²-6ax-16a （a＞0）的图象过B、C两点，点P是线段OC上由O向C移动的动点，线段OP=t（1＜t＜8）
（1）t为何值时，P为圆心OP为半径的圆与l₁相切？
（2）设抛物线对称轴与直线l₁相交于M，请在x轴上求一点N．使△AMN的周长最小．
（3）设点Q是AC上自C向A移动的一动点，且CQ=OP=t．若△PQC的面积为s，求S与t的函数关系式，当△PQC为等腰三角形时，请直接写出t的值．

Answer 1

分析：（1）过P作l₁的垂线，若⊙P与直线l₁相切，那么P到直线l₁的距离等于⊙P的半径即OP的长，然后通过构建的相似三角形直接求出⊙P的半径即可．
（2）取M关于x轴的对称点，连接该对称点和点A，该直线与x轴的交点即为所求的点N．
（3）首先求出点Q的坐标，然后能求出PQ的长；①以CP为底、Q的纵坐标的绝对值为高能得到关于s、t的函数关系式；②用t列出线段CP、CQ、PQ的长，若△PQC为等腰三角形，可根据CP=CQ或CQ=PQ或CP=PQ三种情况列方程求出t的值．

解答：解：（1）抛物线的解析式中，当y=0时，0=a（x²-6x-16），解得：x₁=-2，x₂=8；
∴B（-2，0）、C（8，0）．
过P作PD⊥AC于D，若⊙P与直线l₁相切，则 PD=OP=t；
易知Rt△CPD∽Rt△CAO
∴

PD

OA

=

PC

AC

，即

t

6

=

8-t

10

解得：t=3．

（2）由（1）知：抛物线的对称轴 x=3；
由A（0，6）、C（8，0）得：直线AC y=-

3

4

x+6，则 M（3，

15

4

）．
△AMN中，AM长为定值，若△AMN的周长最小，那么 AN+MN 的值最小；
取点M关于x轴的对称点M'，则M'（3，-

15

4

）；
设直线AM'的解析式为：y=kx+6，则：
3k+6=-

15

4

，k=-

13

4

∴直线AM'：y=-

13

4

x+6
当y=0时，x=

24

13

；即 N（

24

13

，0）．

（3）过Q作QE⊥x轴于点E，则 QE=

3

5

QE=

3

5

t，CE=

4

5

QC=

4

5

t，OE=OC-CE=8-

4

5

t；
∴Q（8-

4

5

t，

3

5

t）．
①PC=OC-OP=8-t；
则 S=

1

2

PC•QE=

1

2

×（8-t）×

3

5

t=-

3

10

t²+

12

5

t（1＜t＜8）．
②PQ²=（8-

4

5

t-t）²+（

3

5

t）²=

18

5

t²-

144

5

t+64，PC²=（8-t）²=t²-16t+64，CQ²=t²；
当PQ=PC时，

18

5

t²-

144

5

t+64=t²-16t+64，解得：t₁=0（舍去），t₂=

64

13

；
当PQ=CQ时，

18

5

t²-

144

5

t+64=t²，解得：t₁=8（舍去），t₂=

40

13

；
当PC=CQ时，t²-16t+64=t²，解得：t=4．
∴当△PQC为等腰三角形时，t₁=

64

13

、t₂=

40

13

、t₃=4．

点评：该二次函数综合题涵盖了直线与圆的位置关系、图形面积的求法以及等腰三角形的判定等知识．（3）题在判定等腰三角形时，要明确不同的腰和底进行分类讨论，以免漏解．