题目内容
15.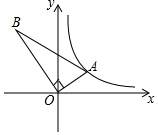 如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | 3 | B. | -3 | C. | -$\frac{9}{4}$ | D. | -$\frac{9}{2}$ |
分析 过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,由同角的余角相等可得出∠OBD=∠AOC,结合∠BDO=∠OCA可证出△OBD∽△AOC,根据相似三角形的性质可得出OD=$\frac{3}{2}$AC、BD=$\frac{3}{2}$OC,再根据反比例函数图象上点的坐标特征可得出OC•AC=2、OD•BD=-k,代入OD=$\frac{3}{2}$AC、BD=$\frac{3}{2}$OC可求出k值.
解答 解:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,如图所示.
∵∠BOD+∠OBD=90°,∠BOD+∠AOC=90°,
∴∠OBD=∠AOC.
∵∠BDO=∠OCA,
∴△OBD∽△AOC,
∴$\frac{OD}{AC}$=$\frac{BD}{OC}$=$\frac{OB}{AO}$=$\frac{3}{2}$,
∴OD=$\frac{3}{2}$AC,BD=$\frac{3}{2}$OC.
∵点A在反比例函数y=$\frac{2}{x}$的图象上,点B在反比例函数y=$\frac{k}{x}$的图象上,
∴OC•AC=2,OD•BD=-k,
解得:k=-$\frac{9}{2}$.
故选D.
点评 本题考查了相似三角形的判定与性质以及反比例函数图象上点的坐标特征,根据相似三角形的性质找出OD=$\frac{3}{2}$AC、BD=$\frac{3}{2}$OC是解题的关键.

练习册系列答案
相关题目
6.若a>b,则下列不等式成立的是( )
| A. | a-3<b-3 | B. | a>b-1 | C. | $\frac{a}{4}<\frac{b}{4}$ | D. | -2a>-2b |
7. 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),一次函数y=-2x+b与线段AB有公共点,则b的取值范围是( )
如图,在平面直角坐标系xOy中,A(1,1),B(2,2),一次函数y=-2x+b与线段AB有公共点,则b的取值范围是( )
 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),一次函数y=-2x+b与线段AB有公共点,则b的取值范围是( )
如图,在平面直角坐标系xOy中,A(1,1),B(2,2),一次函数y=-2x+b与线段AB有公共点,则b的取值范围是( )| A. | 3≤b≤6 | B. | 3≤b≤4 | C. | 1≤b≤2 | D. | -2≤b≤-1 |
19.30000000用科学记数法表示为( )
| A. | 3×108 | B. | 0.3×108 | C. | 3×106 | D. | 3×107 |
5.山西的风景独特而优美,旅游资源精彩又丰富,文化旅游产业成为山西七大非煤产业之首.2015年,陕西省旅游总收入3447.5亿元,同比增长21.11%,旅游业已成为全省最具活力的产业之一,数据3447.5亿元用科学记数法可表示为( )
| A. | 34.475×1010元 | B. | 3.4475×1010元 | C. | 34.475×1011元 | D. | 3.4475×1011元 |
2.函数y=3x+m-5,若y是x的正比例函数,则常数m的值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 15 |