题目内容
4.暑假期间,某剧院举行专场音乐会,成人票每张20元,学生票每张5元,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%收款.向阳中学4名老师带领若干名(不少于4人)学生听音乐会,设学生人数为x,付款总金额为y(元).(1)分别建立两种优惠方案中y与x的函数关系式;
(2)确定最节省钱的购票方案.
分析 (1)首先根据优惠方案①:付款总金额=购买成人票金额+除去4人后的学生票金额;
优惠方案②:付款总金额=(购买成人票金额+购买学生票金额)×打折率,列出y关于x的函数关系式,
(2)根据(1)的函数关系式求出当两种方案付款总金额相等时,购买的票数.再就三种情况讨论.
解答 解:(1)按优惠方案1可得
y1=20×4+(x-4)×5=5x+60(x≥4),
按优惠方案2可得
y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)因为y1-y2=0.5x-12(x≥4),
①当y1-y2=0时,得0.5x-12=0,解得x=24,
∴当购买24张票时,两种优惠方案付款一样多.
②当y1-y2<0时,得0.5x-12<0,解得x<24,
∴4≤x<24时,y1<y2,优惠方案1付款较少.
③当y1-y2>0时,得0.5x-12>0,解得x>24,
当x>24时,y1>y2,优惠方案2付款较少.
点评 本题考查了一次函数的运用.解决本题的关键是根据题意正确列出两种方案的解析式,进而计算出临界点x的取值,再进一步讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.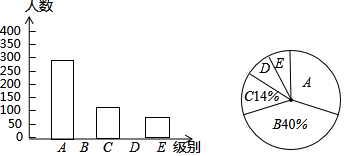 某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.
某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.
请根据图表信息解答下列问题:
(1)统计表中的m=400,n=100,并请补全条形统计图;
(2)扇形统计图中“D”所对应的圆心角的度数是36°;
(3)若该市约有120万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
 某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.
某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.| 组别 | 获取新闻的最主要途径 | 人数 |
| A | 电脑上网 | 280 |
| B | 手机上网 | m |
| C | 电视 | 140 |
| D | 报纸 | n |
| E | 其它 | 80 |
(1)统计表中的m=400,n=100,并请补全条形统计图;
(2)扇形统计图中“D”所对应的圆心角的度数是36°;
(3)若该市约有120万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
15.若多项式x2-2(k-1)x+4是一个完全平方式,则k的值为( )
| A. | 3 | B. | -1 | C. | 3或0 | D. | 3或-1 |
15.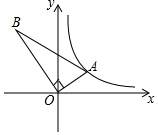 如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
 如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | 3 | B. | -3 | C. | -$\frac{9}{4}$ | D. | -$\frac{9}{2}$ |
10. 如图,直线y1=k1x+b1与直线y2=k2x+b2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集为( )
如图,直线y1=k1x+b1与直线y2=k2x+b2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集为( )
 如图,直线y1=k1x+b1与直线y2=k2x+b2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集为( )
如图,直线y1=k1x+b1与直线y2=k2x+b2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集为( )| A. | x>l | B. | x<l | C. | x>2 | D. | x<2 |
 如图,在平面直角坐标系中,直线y=kx+b与x轴交于点B(3,0),与y轴交于点C(0,$\frac{3}{2}$),
如图,在平面直角坐标系中,直线y=kx+b与x轴交于点B(3,0),与y轴交于点C(0,$\frac{3}{2}$),