题目内容
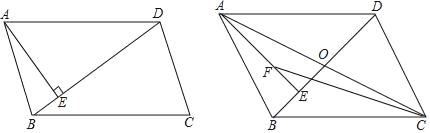
【题目】如图,在![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是弧
是弧![]() 的中点,
的中点,![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() .连接
.连接![]() ,关于下列结论:①
,关于下列结论:①![]()
![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的外心,其中正确结论是( )
的外心,其中正确结论是( )
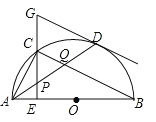
A.①②B.①③C.②③D.①②③
【答案】C
【解析】
由于![]() 与
与![]() 不一定相等,根据圆周角定理可知①错误;连接OD,利用切线的性质,可得出∠GPD=∠GDP,利用等角对等边可得出GP=GD,可知②正确;先由垂径定理得到A为
不一定相等,根据圆周角定理可知①错误;连接OD,利用切线的性质,可得出∠GPD=∠GDP,利用等角对等边可得出GP=GD,可知②正确;先由垂径定理得到A为![]() 的中点,再由C为
的中点,再由C为![]() 的中点,得到
的中点,得到![]() ,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ为直角,由等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,可知③正确;
,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ为直角,由等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,可知③正确;
∵在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,
∴![]() =
=![]() ≠
≠![]() ,
,
∴∠BAD≠∠ABC,故①错误;
连接OD,
则OD⊥GD,∠OAD=∠ODA,
∵∠ODA+∠GDP=90![]() ,∠EPA+∠EAP=∠EAP+∠GPD=90
,∠EPA+∠EAP=∠EAP+∠GPD=90![]() ,
,
∴∠GPD=∠GDP;
∴GP=GD,故②正确;
∵弦CF⊥AB于点E,
∴A为![]() 的中点,即
的中点,即![]() ,
,
又∵C为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴∠CAP=∠ACP,
∴AP=CP.
∵AB为圆O的直径,
∴∠ACQ=90![]() ,
,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故③正确;
故选C.

练习册系列答案
相关题目