题目内容
【题目】抛物线l1：y＝x2+bx+c与它的对称轴x＝﹣2交于点A，且经过点B（0，﹣2）．
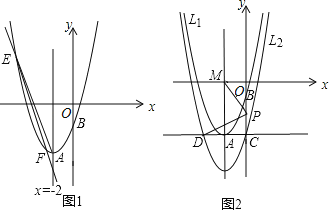
（1）求抛物线l1的解析式；
（2）如图1，直线y＝kx+2k﹣8（k＜0）与抛物线l1交于点E，F，若△AEF的面积为
，求k的值；
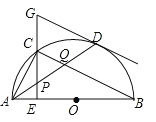
（3）如图2，将抛物线l1向下平移n（n＞0）个单位长度得到抛物线l2，抛物线l2与y轴交于点C，过点C作x轴的平行线交抛物线l2于另一点D；抛物线l2的对称轴与x轴的交于点M，P为线段OC上一点，若△POM与△PCD相似，并且符合该条件的点P有且只有2个，求n的值及相应点P的坐标．
【答案】（1）y＝x2+4x﹣2；（2）k＝﹣4；（3）当n＝4
﹣2时，点P的坐标为（0，﹣2）和（0，﹣
）；当n＝4时，点P坐标为（0，﹣2）和（0，﹣4）．
【解析】
（1）待定系数法求解可得；
（2）设直线y=kx+2k-8与抛物线l1的对称轴交点为G，则G（-2，-8），由顶点A坐标知AG=2，由S△AEF=S△AGE-S△AGF=
AG（-2-xE）-AG（-2-xF）=AG（xF-xE）=2知xF-xE=2，再联立得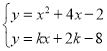
，消去y整理得x2+（4-k）x-2k+6=0，据此知
，继而得出xF-xE=
，据此可得关于k的方程，解之可得答案；
（3）分△PCD∽△MOP和△PCD∽△POM得出t关于n的关系式，再根据符合该条件的点P有且只有两个，进一步求解可得．
解：（1）∵y＝x2+bx+c与它的对称轴x＝﹣2交于点A，且经过点B（0，﹣2）
∴可得
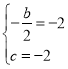，解得
，
∴抛物线l1的解析式为y＝x2+4x﹣2．
（2）如图1，设直线y＝kx+2k﹣8与抛物线l1的对称轴交点为G，则G（﹣2，﹣8），
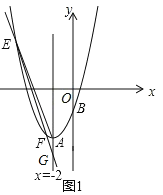
又可得抛物线l1的顶点A（﹣2，﹣6），
∴AG=2，
S△AEF=S△AGE﹣S△AGF
又∵S△AEF＝2，AG＝2，
∴xF﹣xE＝2，
将抛物线l1与直线y＝kx+2k﹣8联立得，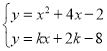
消去y得x2+4x﹣2＝kx+2k﹣8，
整理得x2+（4﹣k）x﹣2k+6＝0，得，
∴xF﹣xE＝，
∴
，
解得k＝±4，
又k＜0，
∴k＝﹣4．
（3）设抛物线l2的解析式为y＝x2+4x﹣2﹣m，
∴C（0，﹣2﹣n），D（﹣4，﹣2﹣n），M（﹣2，0）
设P（0，t）．
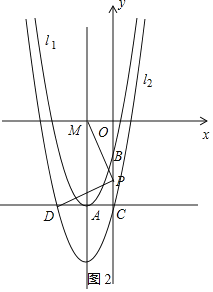
①当△PCD∽△MOP时，
，
∴
，
∴t2+（n+2）t+8＝0；
②当△PCD∽△POM时，
，
∴
，
∴t=
；
（Ⅰ）当方程①有两个相等实数根时，
△＝（n+2）2﹣4×1×8＝0，
解得n＝±4﹣2，
又n＞0，
∴n＝4﹣2，
此时方程①有两个相等实根t1＝t2＝﹣2，方程②有一个实数根t=
；
∴n＝4﹣2，
此时点P的坐标为（0，﹣2）和（0，）；
（Ⅱ）当方程①有两个不相等的实数根时，
把②代入①，得：
，即（n+2）2＝36，
解得n1＝4，n2＝﹣8，
又n＞0，
∴n＝4，
此时方程①有两个不相等的实数根，t1＝﹣2，t2＝﹣4，方程①有一个实数根t＝﹣2；
∴n＝4，
此时点P坐标为（0，﹣2）和（0，﹣4），
综上，当n＝4﹣2时，点P的坐标为（0，﹣2）和（0，）；当n＝4时，点P坐标为（0，﹣2）和（0，﹣4）．
