题目内容
 如图,△ABC中,∠C=90°,BD平分∠ABC,DC=4,AB=10,则△DAB的面积为
如图,△ABC中,∠C=90°,BD平分∠ABC,DC=4,AB=10,则△DAB的面积为考点:角平分线的性质
专题:几何图形问题
分析:过点D作DE⊥AB于点E,根据角的平分线上的点到角的两边的距离相等,得DE=DC=4,再根据三角形的面积计算公式得出△ABD的面积.
解答:解:如图,过点D作DE⊥AB于点E,
∵BD平分∠ABC,
又∵DE⊥AB,DC⊥BC
∴DE=DC=4
∴△ABD的面积=
•AB•DE=
×10×4=20
故答案为20.

∵BD平分∠ABC,
又∵DE⊥AB,DC⊥BC
∴DE=DC=4
∴△ABD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为20.
点评:本题主要考查了角平分线的性质与三角形的面积计算公式.作出辅助线是正确解答本题的关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、2m+3n=5mn | ||||||
| B、(x2)3=x5 | ||||||
| C、(a-b)2=a2-b2 | ||||||
D、
|
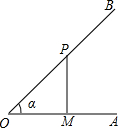 如图,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值为
如图,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值为 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=4cm,则OE的长为
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=4cm,则OE的长为


