题目内容
7.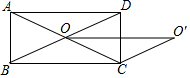 如图,矩形ABCD的对角线AC、BD交于点O,∠AOB=40°.
如图,矩形ABCD的对角线AC、BD交于点O,∠AOB=40°.(1)求∠OCB的度数.
(2)将线段CO绕点C顺时针旋转α度,当α为何值时,四边形OBCO′为平行四边形时,证明你的结论.
分析 (1)只要证明△OBC是等腰三角形即可解决问题.
(2)当CO′∥BO时,四边形OBCO′为平行四边形,由此即可解决问题.
解答  解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OD=OB,
∴∠OBC=∠OCB,
∵∠AOB=∠OBC+∠OCB=40°,
∴∠OCB=20°.
(2)当α=140°时,四边形OBCO′为平行四边形.
理由:∵∠AOB=40°,
∴∠BOC=140°,∵∠OCO′=140°,
∴∠BOC=∠OCO′,
∴OB∥CO′,
∵CO′=CO=OB,
∴四边形OBCO′为平行四边形.
点评 本题考查矩形的性质、平行四边形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.下列调查中,适合用“普查”方式的是( )
| A. | 调查某型号节能灯泡的使用寿命 | |
| B. | 调查某品牌手机的市场占有率 | |
| C. | 调查我校初一(1)班的男女同学的比例 | |
| D. | 调查电视剧《芈月传》在全国的收视率 |
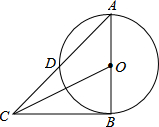 如图,AB是⊙O直径,AD是弦,过B点的切线与AD的延长线交于点C,若AD=CD,求sin∠OCA的值.
如图,AB是⊙O直径,AD是弦,过B点的切线与AD的延长线交于点C,若AD=CD,求sin∠OCA的值.