题目内容
1.若$\sqrt{x-2}$+(y-$\frac{1}{2}$)2=0,则$\frac{1}{\sqrt{x}}$+$\sqrt{y}$=$\sqrt{2}$.分析 利用算术平方根与二次幂的非负性求解即可.
解答 解:∵$\sqrt{x-2}$+(y-$\frac{1}{2}$)2=0,
且:$\sqrt{x-2}$≥0,(y-$\frac{1}{2}$)2≥0,
∴x-2=0,y-$\frac{1}{2}$=0,
∴x=2,y=$\frac{1}{2}$,
则$\frac{1}{\sqrt{x}}$+$\sqrt{y}$=$\frac{1}{\sqrt{2}}+\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}$=$\sqrt{2}$
故答案为:$\sqrt{2}$
点评 本题考查了二次根式的化简求值问题、偶次方及算术平方根的非负性问题,解题的关键是掌握偶次方及算术平方根的非负性的意义.

练习册系列答案
相关题目
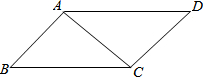 已知:如图,AB⊥AC,DC⊥AC,AD=BC,则根据HL公理,可得△ABC≌△CDA.
已知:如图,AB⊥AC,DC⊥AC,AD=BC,则根据HL公理,可得△ABC≌△CDA.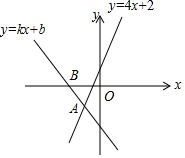 如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式(k-4)x<2-b的解集为x>-1.
如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式(k-4)x<2-b的解集为x>-1.