题目内容
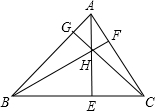 锐角三角形ABC的3条高线相交于点H,其中三角形的个数共有
锐角三角形ABC的3条高线相交于点H,其中三角形的个数共有
- A.12个
- B.15个
- C.16个
- D.18个
C
分析:题中有三条高,则有6个直角,每一个直角对应两个直角三角形,共12个直角三角形,还有三个钝角三角形和原来的一个锐角三角形,于是答案可得.
解答:图中有6个直角,每一个直角对应两个直角三角形,
共有12个直角三角形:△AEB、△AEC、△HEB、△HEC、△BFC、△BFA、△HFC、△HFA、△CGA、△CGB、△HGA、△HGB;
三个钝角三角形:△BHA、△CHA、△CHB;
原来的一个锐角三角形:△ABC;
共有16个三角形.
故选C.
点评:本题考查了三角形的角平分线、中线和高的相关知识;依据直角这个思路找到12个直角三角形是正确解答本题的关键.
分析:题中有三条高,则有6个直角,每一个直角对应两个直角三角形,共12个直角三角形,还有三个钝角三角形和原来的一个锐角三角形,于是答案可得.
解答:图中有6个直角,每一个直角对应两个直角三角形,
共有12个直角三角形:△AEB、△AEC、△HEB、△HEC、△BFC、△BFA、△HFC、△HFA、△CGA、△CGB、△HGA、△HGB;
三个钝角三角形:△BHA、△CHA、△CHB;
原来的一个锐角三角形:△ABC;
共有16个三角形.
故选C.
点评:本题考查了三角形的角平分线、中线和高的相关知识;依据直角这个思路找到12个直角三角形是正确解答本题的关键.

练习册系列答案
相关题目
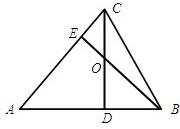 9、如图,锐角三角形ABC的高CD和高BE相交于O,则与△DOB相似的三角形个数是( )
9、如图,锐角三角形ABC的高CD和高BE相交于O,则与△DOB相似的三角形个数是( )