题目内容
15．下列命题中真命题是（ ）| A． | 平行四边形的对角线相等 | B． | 正方形的对角线相等 | ||
| C． | 菱形的对角线相等 | D． | 矩形的对角线互相垂直 |
分析 根据平行四边形的性质对A进行判断；根据正方形的性质对B进行判断；根据菱形的性质对C进行判断；根据矩形的性质对D进行判断．
解答 解：A、平行四边形的对角线互相平分，所以A选项错误；
B、正方形的对角线相等，所以B选项正确；
C、菱形的对角线互相垂直平分，所以C选项错误；
D、矩形的对角线相等，所以D选项错误．
故选B．
点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．
练习册系列答案
阅读快车系列答案
相关题目
5．一个边长为2的正多边形的内角和是其外角和的2倍，则这个正多边形的外接圆半径是（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | 1 | D． | 21 |
6．
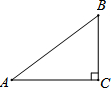已知，如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，则sinB的值是（ ）
已知，如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，则sinB的值是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
10．下列计算中，正确的是（ ）
| A． | ${（{2\sqrt{3}}）^2}=2×3=6$ | B． | $\frac{{\sqrt{8}}}{2}=\sqrt{4}=2$ | C． | $\sqrt{（-9）×（-4）}$=$\sqrt{36}$=6 | D． | $\sqrt{9+16}=\sqrt{9}+\sqrt{16}$ |
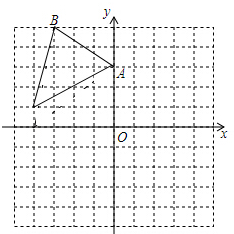如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（0，3），B（-3，5），C（-4，1）．把△ABC向右平移2个单位，再向下平移3个单位得到△A1B1C1．