题目内容
如图,一次函数的图象与反比例函数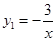 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当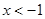 时,一次函数值大于反比例函数值,当
时,一次函数值大于反比例函数值,当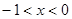 时,一次函数值小于反比例函数值.
时,一次函数值小于反比例函数值.
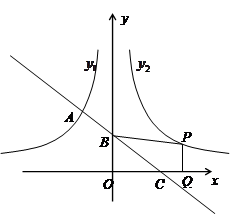
(1)求一次函数的解析式;
(2)设函数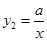 (x>0)的图象与
(x>0)的图象与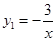 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在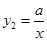 (x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
(x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
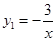 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当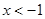 时,一次函数值大于反比例函数值,当
时,一次函数值大于反比例函数值,当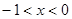 时,一次函数值小于反比例函数值.
时,一次函数值小于反比例函数值.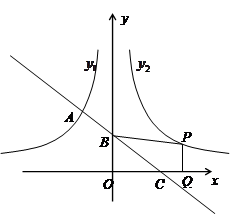
(1)求一次函数的解析式;
(2)设函数
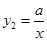 (x>0)的图象与
(x>0)的图象与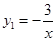 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在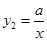 (x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
(x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.(1)一次函数解析式为y= –x+2. (2)P( ,
, )
)
 ,
, )
)解(1)∵x< –1时,一次函数值大于反比例函数值,当-1<x<0,时,一次函数值小于反比例函数值.
∴A点的横坐标是–1,∴A(–1,3)-------1分
设一次函数解析式为y= kx+b,因直线过A、C
则 ,解之得:
,解之得: 
∴一次函数解析式为y= –x+2 -------3分
(2)∵y2 = (x>0)的图象与y1=" –"
(x>0)的图象与y1=" –"  (x<0)的图象y轴对称,
(x<0)的图象y轴对称,
∴y2 = (x>0) -------4分
(x>0) -------4分
∵B点是直线y= –x+2与y轴的交点,∴B (0,2) -------5分
设P(n, ),n>2 S四边形BCQP –S△BOC =2
),n>2 S四边形BCQP –S△BOC =2
∴ ( 2+
( 2+  )n–
)n–  ´2´2 = 2,n =
´2´2 = 2,n =  , -------7分
, -------7分
∴P( ,
, ) -------8分
) -------8分
∴A点的横坐标是–1,∴A(–1,3)-------1分
设一次函数解析式为y= kx+b,因直线过A、C
则
 ,解之得:
,解之得: 
∴一次函数解析式为y= –x+2 -------3分
(2)∵y2 =
 (x>0)的图象与y1=" –"
(x>0)的图象与y1=" –"  (x<0)的图象y轴对称,
(x<0)的图象y轴对称,∴y2 =
 (x>0) -------4分
(x>0) -------4分∵B点是直线y= –x+2与y轴的交点,∴B (0,2) -------5分
设P(n,
 ),n>2 S四边形BCQP –S△BOC =2
),n>2 S四边形BCQP –S△BOC =2∴
 ( 2+
( 2+  )n–
)n–  ´2´2 = 2,n =
´2´2 = 2,n =  , -------7分
, -------7分∴P(
 ,
, ) -------8分
) -------8分
练习册系列答案
相关题目
 、
、 在第一象限的图像如图,
在第一象限的图像如图, ,过
,过 ,作
,作 轴的平行线交
轴的平行线交 , 交
, 交 轴于
轴于 ,若
,若 ,则
,则
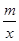 相交于C、D两点,且点D的坐标为(1,6).
相交于C、D两点,且点D的坐标为(1,6).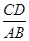 的值为 .
的值为 .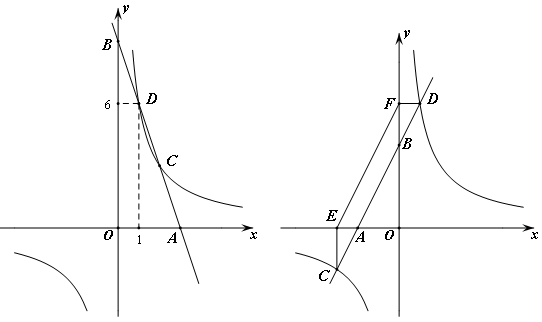
 与
与 的图象交于A、B两点,过点A作AC垂直于
的图象交于A、B两点,过点A作AC垂直于 轴,垂足为C,则△BOC的面积为
轴,垂足为C,则△BOC的面积为

 、
、 ,则
,则
 图象上有两点
图象上有两点 、
、 ,当
,当 时,
时, ,则
,则 的取值范围是【 】
的取值范围是【 】



 和y=kx+3的图象大致是 ( )
和y=kx+3的图象大致是 ( )
 的面积为9 ,点
的面积为9 ,点 在函数
在函数 的图象上,点
的图象上,点 (
( )是函数
)是函数 分别作
分别作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 、
、 ,若设矩形
,若设矩形 和正方形
和正方形 。
。
 的值;(2)写出
的值;(2)写出 的函数关系和
的函数关系和 是函数 的图象上关于原点对称的两点,
是函数 的图象上关于原点对称的两点, ∥
∥ 轴,
轴, ∥
∥ 轴,△
轴,△

 ,则( )
,则( )



