Question

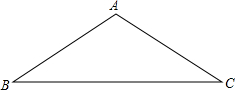在△ABC，∠BAC=120°，AB=AC=8

3

cm，一动点P从B向C以每秒2cm的速度移动，问当P点移到多少秒时，PA与腰垂直？

Answer 1

考点：等腰三角形的性质

专题：分类讨论

分析：首先根据三角形的内角和定理和等腰三角形的两个底角相等求得∠B=∠C=30°．要使PA与腰垂直，则有两种情况：与AB垂直或与AC垂直．根据30°角所对的直角边是斜边的一半以及等角对对边的性质，得：PB=8或16．再根据时间=路程÷速度，得点P移动4秒或8秒．

解答：解：∵∠BAC=120°，AB=AC，
∴∠B=∠C=30°
①当EA⊥AC时，
∵∠C=30°，AC=8

3

，
tan30°=

AE

AC

，
∴AE=ACtan30°=8

3

×

3

3

=8，
∴AE=8，∠AEC=60°，
又∵∠B+∠BAE=∠AEC，
∴∠B=∠BAE=30°，
∴AE=BE=8，
此时P点运动了4秒；
同理②当FA⊥AB与点A时，BF=16，此时P点运动了8秒，
∴当P点移到4秒或8时，PA与腰垂直．

点评：考查了等腰三角形的性质，首先能够分析出有两种情况．然后熟练运用等腰三角形的性质以及直角三角形的性质进行求解．