题目内容
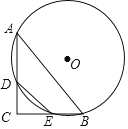
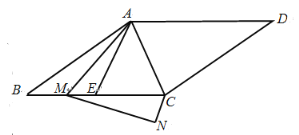
【题目】如图,![]() 的平分线过点
的平分线过点![]() ,以
,以![]() 点为圆心的圆与
点为圆心的圆与![]() 相切于点
相切于点![]() ,
,![]() 为
为![]() 的直径.
的直径.
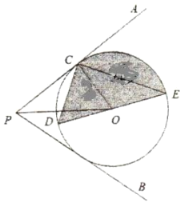
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)若![]() 的半径为
的半径为![]() ,
,![]() ,求阴影部分的面积.
,求阴影部分的面积.
【答案】(1)证明见解析,(2)![]() (3)
(3)![]()
【解析】
(1)过点O作OH⊥PB,证明OH=OC即可;
(2)由圆周角定理求出∠COD=2∠E=50°,由切线求出∠COP的度数,∠COD-∠COP即可得到答案;
(3)在Rt△CDE中,由三角函数先求出∠E的度数为30°,进而求出圆心角∠COE=120°,再由扇形面积公式算出扇形COE的面积,再加上等边△CDO的面积及得到阴影部分的面积.
解:(1)证明:过点O作OH⊥PB于H点,如下图所示:
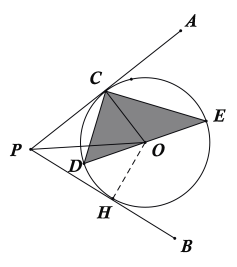
∵AP为圆O的切线,且C为切点
∴CO⊥PC
∵PO为∠APB的角平分线,且CO⊥PC,OH⊥PB
∴OH=OC
故PB是圆O的切线.
(2)∵∠CPO=50°,且CP⊥CO
∴∠COP=90°-50°=40°
又由同弧所对的圆周角是圆心角的一半可知
∠COD=2∠E=2×25°=50°
∴∠POD=∠COD-∠COP=50°-40°=10°.
故答案为:10°.
(3)∵DE为圆O的直径
∴在Rt△DEC中,![]()
∴∠E=30°
∴∠COE=180°-30°-30°=120°
∴扇形COE的面积为:![]()
∴△CDO的面积为:![]()
故阴影部分的面积为:![]()
故答案为:![]()

练习册系列答案
相关题目