题目内容
5.计算:(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
(2)($\sqrt{50}$-$\sqrt{8}$)$÷\sqrt{2}$.
分析 (1)先把各个二次根式进行化简,合并同类二次根式即可;
(2)先把各个二次根式进行化简,合并同类二次根式,再根据二次根式的除法法则计算即可.
解答 解:(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$=4$\sqrt{3}$-2$\sqrt{3}$+12$\sqrt{3}$=14$\sqrt{3}$;
(2)($\sqrt{50}$-$\sqrt{8}$)$÷\sqrt{2}$=(5$\sqrt{2}$-2$\sqrt{2}$)÷$\sqrt{2}$=3$\sqrt{2}$÷$\sqrt{2}$=3.
点评 本题考查的是二次根式的混合运算,掌握二次根式的性质和二次根式的混合运算法则是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
16.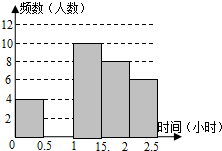 我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
(1)在表格中,a=12,b=0.2;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
 我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.| 时间(小时) | 频数(人数) | 频率 |
| 0≤t<0.5 | 4 | 0.1 |
| 0.5≤t<1 | a | 0.3 |
| 1≤t<1.5 | 10 | 0.25 |
| 1.5≤t<2 | 8 | b |
| 2≤t<2.5 | 6 | 0.15 |
| 合计 | 1 |
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
15. 如图,将直尺和直角三角板按如图方式摆放,已知∠1=35°,则∠2的大小是( )
如图,将直尺和直角三角板按如图方式摆放,已知∠1=35°,则∠2的大小是( )
 如图,将直尺和直角三角板按如图方式摆放,已知∠1=35°,则∠2的大小是( )
如图,将直尺和直角三角板按如图方式摆放,已知∠1=35°,则∠2的大小是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
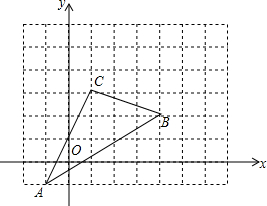 如图,三角形ABC在直角坐标系中,
如图,三角形ABC在直角坐标系中, 如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
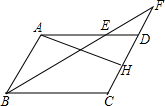 如图,在?ABCD中,AB=4,AD=6,∠ABC的平分线交AD于点E,交CD的延长线于点F.
如图,在?ABCD中,AB=4,AD=6,∠ABC的平分线交AD于点E,交CD的延长线于点F.