题目内容
6.解下列方程组:(1)$\left\{\begin{array}{l}{3x+2y=8}\\{x-2y=4}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y+1}{3}=1}\\{3x+2y=4}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+2y=8①}\\{x-2y=4②}\end{array}\right.$,
①+②得:4x=12,
解得:x=3,
把x=3代入②得:y=-$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-\frac{1}{2}}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{3x-2y=8①}\\{3x+2y=4②}\end{array}\right.$,
①+②得:6x=12,
解得:x=2,
①-②得:-4y=4,
解得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
16. 如图,直线a∥b,△ABC是直角三角形,∠A=90°,∠ABF=24°,则∠ACE等于( )
如图,直线a∥b,△ABC是直角三角形,∠A=90°,∠ABF=24°,则∠ACE等于( )
 如图,直线a∥b,△ABC是直角三角形,∠A=90°,∠ABF=24°,则∠ACE等于( )
如图,直线a∥b,△ABC是直角三角形,∠A=90°,∠ABF=24°,则∠ACE等于( )| A. | 65° | B. | 66° | C. | 67° | D. | 56° |
17.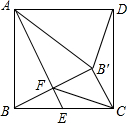 如图,在正方形ABCD中,点E是 BC边的中点,点B′与点B关于AE对称,BB′与AE交
如图,在正方形ABCD中,点E是 BC边的中点,点B′与点B关于AE对称,BB′与AE交
于点F.下列结论错误的是( )
 如图,在正方形ABCD中,点E是 BC边的中点,点B′与点B关于AE对称,BB′与AE交
如图,在正方形ABCD中,点E是 BC边的中点,点B′与点B关于AE对称,BB′与AE交于点F.下列结论错误的是( )
| A. | AB′=AD | B. | ∠ADB′=75° | ||
| C. | ∠CB′D=135° | D. | △FCB′是等腰直角三角形 |
16.某企业的年收入约为700000元,数据“700000”用科学记数法可表示为( )
| A. | 0.7×106 | B. | 7×105 | C. | 7×104 | D. | 70×104 |
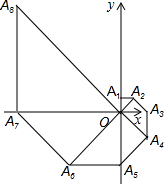 如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2018,则点A2017的坐标为(0,($\sqrt{2}$)2016)或(0,21008).
如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2018,则点A2017的坐标为(0,($\sqrt{2}$)2016)或(0,21008).