题目内容
19．解方程：$\frac{y-2}{y-3}$=$\frac{1}{2-5y}$．分析 分式方程去分母转化为整式方程，求出整式方程的解得到y的值，经检验即可得到分式方程的解．
解答 解：去分母得：2y-5y2-4+10y=y-3，即5y2-11y+1=0，
解得：y=$\frac{11±\sqrt{101}}{10}$，
经检验y=$\frac{11±\sqrt{101}}{10}$都为分式方程的解．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
天天练口算系列答案
相关题目
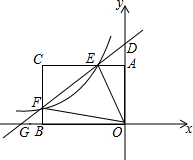如图，矩形AOBC的顶点坐标分别为A（0，3），O（0，0），B（-4，0），C（-4，3）动点F在BC上（不与B、C重合）过点F的反比例函数y=$\frac{k}{x}$的图象与边AB交于点E，直线EF分别与y轴和x轴相交于点D，G
一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$的图象相交，其中的一个交点P在第四象限，PA⊥x轴于点A，PQ⊥y轴于点B，AC=2OC，一次函数的图象分别交x轴、y轴于点C、点D，且且S△DBP=27
4．-3的倒数是（ ）
| A． | -3 | B． | 3 | C． | -$\frac{1}{3}$ | D． | $\frac{1}{3}$ |