题目内容
3. 一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$的图象相交,其中的一个交点P在第四象限,PA⊥x轴于点A,PQ⊥y轴于点B,AC=2OC,一次函数的图象分别交x轴、y轴于点C、点D,且且S△DBP=27
一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$的图象相交,其中的一个交点P在第四象限,PA⊥x轴于点A,PQ⊥y轴于点B,AC=2OC,一次函数的图象分别交x轴、y轴于点C、点D,且且S△DBP=27(1)求一次函数与反比例函数的表达式;
(2)已知点Q与点P、A、C是一个平行四边形的四个顶点,请直接写出点Q的坐标.
分析 (1)令一次函数解析式中x=0,求出对应的y值,确定出D的坐标,得到OD的长,再由已知条件得到OB的长,由OD+OB求出BD的长,在直角三角形BDP中,利用两直角边乘积的一半表示出三角形的面积,将BD及已知的面积代入求出BP的长,确定出P的坐标,由P为一次函数与反比例函数的交点,将P的坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将P的坐标代入反比例函数解析式中求出m的值,确定出反比例函数解析式;
(2)如图所示根据A、P、C的坐标结合平行四边形的性质即可求得.
解答 解:(1)令一次函数解析式y=kx+3中x=0,解得y=3,
∴D坐标为(0,3),即OD=3,
∵PA∥y轴,
∵$\frac{PA}{OD}$=$\frac{AC}{OC}$
又∵AC=2OC,
∴PA=6,
∴OB=6,
∴BD=OD+OB=3+6=9,
∵SRt△BDP=$\frac{1}{2}$BD•BP=$\frac{1}{2}$×9×BP=27,
∴BP=6,
∴P的坐标为(6,-6),
将x=6,y=-6代入一次函数解析式得:-6=6k+3,
解得:k=-$\frac{3}{2}$,
∴一次函数解析式为y=-$\frac{3}{2}$x+3,
将x=6,y=-6代入反比例解析式得:-6=$\frac{m}{6}$,
解得:m=-36,
∴反比例函数的表达式为y=-$\frac{36}{x}$;
(2)如图,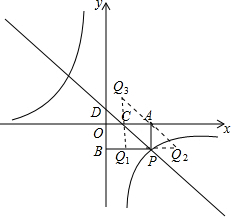
∵A(6,0),P(6,-6),C(2,0),
∴Q(2,-6)或(10,-6)或(2,6).
点评 此题考查了一次函数与反比例函数的交点,以及利用待定系数法求函数解析式,其中利用待定系数法确定出两函数解析式是求两函数交点的关键.

练习册系列答案
相关题目
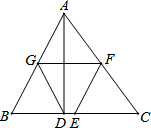 在△ABC中,AD⊥BC于点D,E,F,G分别是BC,AC,BA的中点,求证:四边形DEFG是等腰梯形.
在△ABC中,AD⊥BC于点D,E,F,G分别是BC,AC,BA的中点,求证:四边形DEFG是等腰梯形.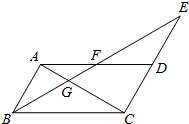 如图,在?ABCD中,延长CD到E,使DE=CD,连接BE,交AD于点F,交AC于点G.
如图,在?ABCD中,延长CD到E,使DE=CD,连接BE,交AD于点F,交AC于点G.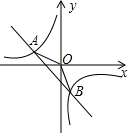 如图,已知A(-4,n),B (2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,则三角形AOB的面积是( )
如图,已知A(-4,n),B (2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,则三角形AOB的面积是( ) 在平面直角坐标系xOy中,抛物线y=ax2+bx+1(a≠0)过点A(-1,0),B(1,1),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=ax2+bx+1(a≠0)过点A(-1,0),B(1,1),与y轴交于点C.