题目内容
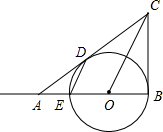 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,求证:DE∥OC.
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,求证:DE∥OC.考点:切线的性质
专题:证明题
分析:首先连接OD,由在△ABC中,∠B=90°,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,易证得Rt△ODC≌Rt△OBC(HL),然后由等腰三角形与三角形外角的性质,证得∠OED=∠BOC,继而证得DE∥OC.
解答: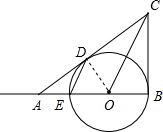 证明:连接OD,
证明:连接OD,
∵AC切⊙O点D,
∴OD⊥AC,
∴∠ODC=∠B=90°,
在Rt△OCD和Rt△OCB中,
∴Rt△ODC≌Rt△OBC(HL),
∴∠DOC=∠BOC;
∵OD=OE,
∴∠ODE=∠OED,
∵∠DOB=∠ODE+∠OED,
∴∠BOC=∠OED,
∴DE∥OC.
 证明:连接OD,
证明:连接OD,∵AC切⊙O点D,
∴OD⊥AC,
∴∠ODC=∠B=90°,
在Rt△OCD和Rt△OCB中,
|
∴Rt△ODC≌Rt△OBC(HL),
∴∠DOC=∠BOC;
∵OD=OE,
∴∠ODE=∠OED,
∵∠DOB=∠ODE+∠OED,
∴∠BOC=∠OED,
∴DE∥OC.
点评:此题考查了切线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
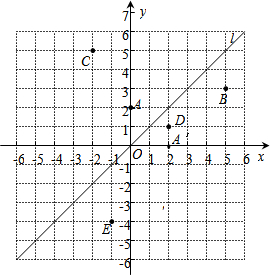 如图,在平面直角坐标系中,直线l的解析式是y=x.
如图,在平面直角坐标系中,直线l的解析式是y=x.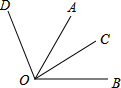 如图,∠AOB=60°,OC平分∠AOB,∠AOD=51°,求∠COD的余角的度数.
如图,∠AOB=60°,OC平分∠AOB,∠AOD=51°,求∠COD的余角的度数. 如图,反比例函数y=
如图,反比例函数y=