题目内容
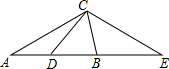 如图,在等腰△ABC中,AB=AC,D是AB的中点,E是AB延长线上一点,且BE=AB,求证:
如图,在等腰△ABC中,AB=AC,D是AB的中点,E是AB延长线上一点,且BE=AB,求证:(1)CE=2CD;
(2)CB平分∠DCE.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)由条件可得出
=
,结合公共角A,可证明△ACD∽△AEC,再由线段比为
,可得出结论;
(2)由(1)相似可得到∠ACD=∠E,结合等腰三角形的底角相等,可得到∠BCE=∠DCB.
| AC |
| AE |
| AD |
| AC |
| 1 |
| 2 |
(2)由(1)相似可得到∠ACD=∠E,结合等腰三角形的底角相等,可得到∠BCE=∠DCB.
解答:证明:(1)∵BE=AB,
∴AE=AB+BE=2AB=2AC,
又∵D是AB的中点,
∴AE=2AD,
故
=
=
,
又∵∠A是公共角,
∴△ACD∽△AEC,
∴
=
=
,
即CE=2CD;
(2)∵△ACD∽△AEC,
∴∠ACD=∠E,
∵AC=AB,
∴∠ACB=∠ABC,
又∵∠ACB=∠ACD+∠DCB,
∠ABC=∠BCE+∠E,
所以∠BCE=∠DCB,
即CB平分∠DCE.
∴AE=AB+BE=2AB=2AC,
又∵D是AB的中点,
∴AE=2AD,
故
| AC |
| AE |
| AD |
| AC |
| 1 |
| 2 |
又∵∠A是公共角,
∴△ACD∽△AEC,
∴
| CD |
| CE |
| AD |
| AC |
| 1 |
| 2 |
即CE=2CD;
(2)∵△ACD∽△AEC,
∴∠ACD=∠E,
∵AC=AB,
∴∠ACB=∠ABC,
又∵∠ACB=∠ACD+∠DCB,
∠ABC=∠BCE+∠E,
所以∠BCE=∠DCB,
即CB平分∠DCE.
点评:本题主要考查三角形相似的判定和性质,利用条件得出线段成比例是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
下列各式:x+1,a≠0,-a,9>2,
,S=
ab,0,其中代数式的个数是( )
| x-y |
| x+y |
| 1 |
| 2 |
| A、5 | B、4 | C、3 | D、2 |
把方程3x+y=5改写成用y的代数式来表示x的形式是( )
| A、y=3x+5 |
| B、y=5-3x |
| C、y=3x-5 |
| D、-y=5-3x |
 如图,△ACE≌△DBF,∠E=∠F,AD=10,BC=4.
如图,△ACE≌△DBF,∠E=∠F,AD=10,BC=4.