��Ŀ����
11��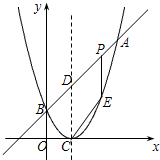 ��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+m��ö��κ�����ͼ����A��B���㣬����A�������Ϊ��3��6������B��y���ϣ�
��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+m��ö��κ�����ͼ����A��B���㣬����A�������Ϊ��3��6������B��y���ϣ���1����m��ֵ��������κ����Ĺ�ϵʽ��
��2��PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��x��Ĵ�����������κ�����ͼ���ڵ�E�����߶�PE�ij�Ϊh����P�ĺ�����Ϊx����h��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��DΪֱ��AB��������κ���ͼ��Գ���Ľ��㣬���߶�AB�ϴ���һ��P��ʹ���ı���DCEP��ƽ���ı��Σ������ʱP������꣮
���� ��1��ֱ�Ӱѵ�A���������ֱ��y=x+m���m��ֵ���ɣ���������κ����Ľ���ʽΪy=a��x-1��2���ٰѵ�A������������a��ֵ���ɵó����ۣ�
��2����P��E�����������ֱ�ΪyP��yE������PE=h=yP-yE���ɵó�h��x֮��ĺ�����ϵʽ��
��3������ƽ���ı��ε����ʵó�PE=DC�����ɵ�D��ֱ��y=x+3�ϵó�D�����꣬�����ɵó����ۣ�
��� �⣺��1���ߵ�A��3��6����ֱ��y=x+m�ϣ�
��6=3+m��
��m=3��
��������κ����Ľ���ʽΪy=a��x-1��2��
�ߵ�A��3��6���ڶ��κ�����ͼ���ϣ�
��6=a��3-1��2�����a=$\frac{3}{2}$��
��������κ����Ľ���ʽΪy=$\frac{3}{2}$��x-1��2����y=$\frac{3}{2}$x2-3x+$\frac{3}{2}$��
��2����P��E�����������ֱ�ΪyP��yE��
��PE=h=yP-yE=��x+3��-��$\frac{3}{2}$x2-3x+$\frac{3}{2}$��=-$\frac{3}{2}$x2+4x+$\frac{3}{2}$����h=-$\frac{3}{2}$x2+4x+$\frac{3}{2}$��0��x��3����
��3�����ı���DCEP��ƽ���ı��Σ�
��PE=DC��
�ߵ�D��ֱ��y=x+3�ϣ�
��D��1��4����
��-$\frac{3}{2}$x2+4x+$\frac{3}{2}$=4�����x1=$\frac{5}{3}$��x2=1����ȥ����
�൱P��$\frac{5}{3}$��$\frac{14}{3}$��ʱ���ı���DCEP��ƽ���ı��Σ�
���� ���⿼����Ƕ��κ����ۺ��⣬�漰���ô���ϵ������һ�κ��������κ����Ľ���ʽ��ƽ���ı��ε��ж������ʵ�֪ʶ���ѶȽϴ�

| A�� | ��������������ͳ������ | B�� | ������0������ͳ�������� | ||
| C�� | ���������������ͦ�ͳ�������� | D�� | ��������������ͳ��ʵ�� |
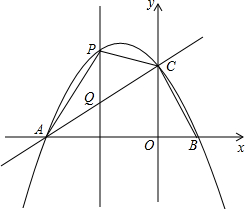 ��ƽ��ֱ������ϵ�У�������y=-$\frac{1}{2}{x^2}$+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����֪A������Ϊ��-3��0����tan��CAB=$\frac{1}{2}$��ֱ��x=m��-1��m��0�����������ڵ�P����ֱ��AC���ڵ�Q��
��ƽ��ֱ������ϵ�У�������y=-$\frac{1}{2}{x^2}$+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����֪A������Ϊ��-3��0����tan��CAB=$\frac{1}{2}$��ֱ��x=m��-1��m��0�����������ڵ�P����ֱ��AC���ڵ�Q��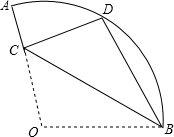 ��ͼ��������OAB�У���AOB=110�㣬������OAB�ع���B��ֱ���۵�����Oǡ������$\widehat{AB}$�ϵĵ�D�������߽�OA�ڵ�C�����ABD=25�㣮
��ͼ��������OAB�У���AOB=110�㣬������OAB�ع���B��ֱ���۵�����Oǡ������$\widehat{AB}$�ϵĵ�D�������߽�OA�ڵ�C�����ABD=25�㣮 ��ͼ��ʾ��AB��CD�ཻ�ڵ�D���ڻ���AC������һ��P��ʹ��P��ֱ��AB��CD�ľ�����ȣ�������ͼ�ۼ�����д��������
��ͼ��ʾ��AB��CD�ཻ�ڵ�D���ڻ���AC������һ��P��ʹ��P��ֱ��AB��CD�ľ�����ȣ�������ͼ�ۼ�����д��������