题目内容
10．
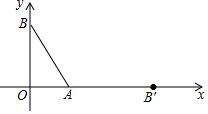如图，在平面直角坐标系中，点A，B的坐标分别是A（3，0），B（0，4），把线段AB绕点A旋转后得到线段AB′，使点B的对应点B′落在x轴的正半轴上，则点B′的坐标是（ ）| A． | （5，0） | B． | （8，0） | C． | （0，5） | D． | （0，8） |
分析 直接利用勾股定理得出AB的长，再利用旋转的性质得出OB′的长，进而得出答案．
解答 解：∵A（3，0），B（0，4），
∴AO=3，BO=4，
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴AB=AB′=5，故OB′=8，
∴点B′的坐标是（8，0）．
故选：B．
点评 此题主要考查了勾股定理以及坐标与图形的性质，正确得出AB′的长是解题关键．
练习册系列答案
相关题目
20．
在数轴上表示有理数a、b的点的位置如图所示，那么下列各式成立的是（ ）
在数轴上表示有理数a、b的点的位置如图所示，那么下列各式成立的是（ ）| A． | a＞b | B． | -a＜b | C． | -b＞a | D． | |a|＜|b| |
1．下列说法正确的是（ ）
| A． | a和0是都是单项式 | B． | 多项式-3a2b+7a2b2的次数是3 | ||
| C． | 单项式$-\frac{2}{3}{a^2}b$的系数为-2 | D． | ${x^2}+\frac{2}{y}$是整式 |
18．
如图，在矩形ABCD中，AB=4，BC=6，将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF，延长DA交FG于点H，则GH的长为（ ）
如图，在矩形ABCD中，AB=4，BC=6，将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF，延长DA交FG于点H，则GH的长为（ ）| A． | 8-4$\sqrt{3}$ | B． | $\frac{8\sqrt{3}}{3}$-4 | C． | 3$\sqrt{3}$-4 | D． | 6-3$\sqrt{3}$ |
15．
将五个相同的小正方体堆成如图所示的物体，它的俯视图是（ ）
将五个相同的小正方体堆成如图所示的物体，它的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
如图，△ABC中，∠B=90°，AB=12，BC=9，半径为1的⊙O的圆心与点B重合，D，E分别为AC与⊙O上的动点．