题目内容
【题目】在![]() 中,以
中,以![]() 为斜边,作直角
为斜边,作直角![]() ,使点
,使点![]() 落在
落在![]() 内,
内,![]() .
.
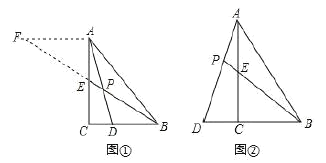
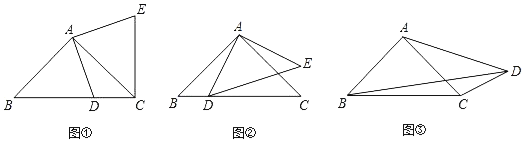
(1)如图1,若![]() ,
,![]() ,
,![]() ,点
,点![]() 分别为
分别为![]() 边的中点,连接
边的中点,连接![]() ,求线段
,求线段![]() 的长;
的长;
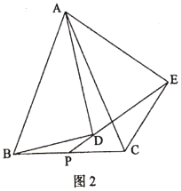
(2)如图2,若![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转一定角度,得到
逆时针旋转一定角度,得到![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.

【答案】(1)6;(2)见详解.
【解析】
(1)在直角三角形中,利用锐角三角函数求出AB,由中位线定理即可得到PM;
(2)先利用等角的余角相等判断出∠BDP=∠PEC,得到△BDP和△CEQ全等,再用三角形的外角得到∠EPC=∠PQC,即可得到结论成立;
(1)解:∵∠ADB=90°,∠BAD=30°,AD=![]() ,
,
∴cos∠BAD=![]() ,
,
∴AB=![]() ,
,
∴AC=AB=12,
∵点P、M分别为BC、AB边的中点,
∴PM=![]() AC=6;
AC=6;
(2)如图2,在ED上截取EQ=PD,

∵∠ADB=90°,
∴∠BDP+∠ADE=90°,
∵AD=AE,
∴∠ADE=∠AED,
∵把△ABD绕点A逆时针旋转一定角度,得到△ACE,
∴∠AEC=∠ADB=90°
∵∠AED+∠PEC=90°,
∴∠BDP=∠PEC,
在△BDP和△CEQ中,
 ,
,
∴△BDP≌△CEQ,
∴BP=CQ,∠DBP=∠QCE,
∵∠CPE=∠BDP+∠DBP,∠PQC=∠PEC+∠QCE,
∴∠EPC=∠PQC,
∴PC=CQ,
∴BP=CP.

练习册系列答案
相关题目