Question

【题目】在中，，是边上的中线，点在射线上.

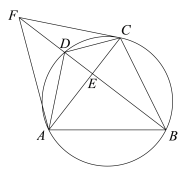
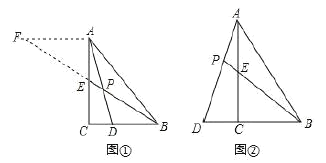
猜想:如图①，点在边上， ，与相交于点，过点作，交的延长线于点，则的值为 .

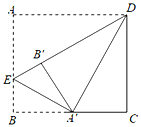
探究:如图②，点在的延长线上，与的延长线交于点， ，求的值.

应用:在探究的条件下，若，，则 .

Answer 1

【答案】猜想: ；探究:6.

【解析】

猜想：如图①，证明，利用相似比得，则，再证明，然后利用相似比即可得到；

探究：过点作作，交的延长线于点，如图②，设，则，先证明，得到，即，再证明，从而利用相似比得；

应用：先利用勾股定理得，则，再证明，利用相似比得到，然后利用比例的性质计算BP的长．

解:猜想:如图①

∵是边上的中线，

∴，

∵，

∴，

∴，

∵，

∴，

∵，

∴，

∴；

探究:过点作作，交的延长线于点，如图②，

设，则，

∴，

∴，

∴，即，

∵，

∴，

∴；

应用：，，

在中，，

∴，

∵，

∴，

∴，

∴.

故答案为，6.