题目内容
10．因式分解：6（x-3）2-24=6（x-1）（x-5）．分析 原式提取6，再利用平方差公式分解即可．
解答 解：原式=6[（x-3）2-4]=6（x-3+2）（x-3-2）=6（x-1）（x-5），
故答案为：6（x-1）（x-5）
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
20．如图，下列推理正确的是（ ）
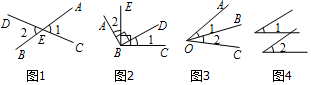
①∵直线AB、CD相交于点E（如图1）∴∠1=2
②∵∠ABD=∠EBC=Rt∠（如图2）∴∠1=∠2
③∵OB平分∠AOC（如图3）∴∠1=∠2
④∵∠1=28.3°，∠2=28°30'（如图4）∴∠1=∠2．
①∵直线AB、CD相交于点E（如图1）∴∠1=2
②∵∠ABD=∠EBC=Rt∠（如图2）∴∠1=∠2
③∵OB平分∠AOC（如图3）∴∠1=∠2
④∵∠1=28.3°，∠2=28°30'（如图4）∴∠1=∠2．
| A． | ①③ | B． | ①②③ | C． | ①③④ | D． | ①②③④ |
5．
如图所示的几何体的俯视图是（ ）
如图所示的几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
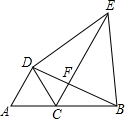如图，点C在线段AB上，△DAC和△DBE都是等边三角形．
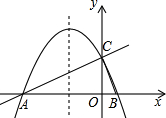如图，在平面直角坐标系xoy中，直线y=$\frac{1}{2}$x+2与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$，且经过A，C两点，与x轴的另一个交点为点B．
20．小明在解方程3a-2x=11（x是未知数）时，误将-2x看成了+2x，得到的解为x=-2，请聪明的你帮小明算一算，方程的正确解为（ ）
| A． | x=1 | B． | x=2 | C． | x=0 | D． | x=-3 |