题目内容
18.已知函数y=mx2+5x-10的图象与x轴有交点,则m的取值范围是m≥-$\frac{5}{8}$.分析 分两种情况考虑:当m不为0时,函数为二次函数,找出二次项系数为m,一次项系数为5,常数项为-10,计算出b2-4ac,根据b2-4ac≥0,即可得出二次函数图象与x轴有交点;当m=0时,将m=0代入得到y=5x-10,此时函数为一次函数,得到此时函数与x轴有1个交点,即可得到m的取值范围.
解答 解:分两种情况考虑:
(i)m≠0时,函数y=mx2+5x-10为二次函数,
∵函数y=mx2+5x-10的图象与x轴有交点,
∴b2-4ac=25+40m≥0,
∴m≥-$\frac{5}{8}$;
(ii)当m=0时,函数解析式为y=5x-10,是一次函数,
∴此时y=5x-10与x轴有一个交点,
综上所述,m≥-$\frac{5}{8}$时,函数y=mx2+5x-10的图象与x轴有交点.
故答案为:m≥-$\frac{5}{8}$.
点评 此题考查了抛物线与x轴的交点,二次函数y=ax2+bx+c与x轴的交点由b2-4ac来决定,当b2-4ac<0,抛物线与x轴没有交点;当b2-4ac=0,抛物线与x轴只有一个交点;当b2-4ac>0时,抛物线与x轴有两个交点.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.下列作图语句正确的是( )
| A. | 作线段AB,使α=AB | B. | 延长线段AB到C,使AC=BC | ||
| C. | 作∠AOB,使∠AOB=∠α | D. | 以O为圆心作弧 |
 图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.
图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.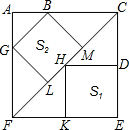 如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2
如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2