题目内容
将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,如图①所示.已知∠CGD=42°.
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示.点H,B的读数分别为4,13.4,求BC的长.(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)

(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示.点H,B的读数分别为4,13.4,求BC的长.(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)

考点:解直角三角形的应用
专题:
分析:(1)先根据直角三角形的两锐角互为求出∠CDG的度数,再根据两直线平行,同位角相等求出∠CEF;
(2)根据度数求出HB的长度,再根据∠CBH=∠CGD=42°,利用42°的余弦值进求解.
(2)根据度数求出HB的长度,再根据∠CBH=∠CGD=42°,利用42°的余弦值进求解.
解答:解:(1)∵∠CGD=42°,∠C=90°,
∴∠CDG=90°-42°=48°,
∴∠CEF=∠CDG=48°;
(2)∵点H、B的读数分别为4、13.4,
∴HB=13.4-4=9.4,
∴BC=HBcos42°=9.4×0.74≈6.956(m),
答:BC的长为6.956m.
∴∠CDG=90°-42°=48°,
∴∠CEF=∠CDG=48°;
(2)∵点H、B的读数分别为4、13.4,
∴HB=13.4-4=9.4,
∴BC=HBcos42°=9.4×0.74≈6.956(m),
答:BC的长为6.956m.
点评:本题考查了解直角三角形与平行线的性质,直角三角形两锐角互余的性质,三角形的一个外角等于与它不相邻的两个内角的和,综合性较强,但难度不大,仔细分析图形并认真计算即可.

练习册系列答案
相关题目
若式子
在实数范围内有意义,则x的取值范围是( )
| ||
| x |
| A、x≥-1 |
| B、x≠0 |
| C、x>-1且x≠0 |
| D、x≥-1且x≠0 |
由四舍五入法得到的近似数2.37×103,下列说法正确的是( )
| A、精确到百分位 |
| B、精确到个位 |
| C、精确到十位 |
| D、精确到千位 |
一个扇形的圆心角为120°,半径为15cm,则它的弧长为( )
| A、5πcm | B、10πcm |
| C、15πcm | D、20πcm |
 如图,直线a∥b.直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=32°,则∠2=
如图,直线a∥b.直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=32°,则∠2=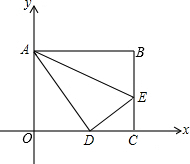 如图,平面直角坐标系中,矩形OABC的顶点B(10,8),点A在y轴上,点C在x轴上,E为BC上一点,把△ABE沿ZE折叠,点B落在OC上的D处.
如图,平面直角坐标系中,矩形OABC的顶点B(10,8),点A在y轴上,点C在x轴上,E为BC上一点,把△ABE沿ZE折叠,点B落在OC上的D处. 已知∠α,∠β,利用尺规作∠AOB=∠α-∠β.
已知∠α,∠β,利用尺规作∠AOB=∠α-∠β.