题目内容
6.直线l:y=mx-m+1(m为常数,且m≠0)与坐标轴交于A、B两点,若△AOB(O是原点)的面积恰为2,则符合要求的直线l有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 根据一次函数图象上点的坐标特征求出点A、B的坐标,利用三角形的面积公式结合△AOB的面积恰为2,即可得出关于m含绝对值符号的方程,解之即可得出结论.
解答 解:当x=0时,y=mx-m+1=1-m,
∴直线l与y轴的交点A的坐标为(0,1-m);
当y=mx-m+1=0时,x=1-$\frac{1}{m}$,
∴直线l与x轴的交点B的坐标为(1-$\frac{1}{m}$,0).
∵△AOB(O是原点)的面积恰为2,
∴$\frac{1}{2}$|1-m||1-$\frac{1}{m}$|=2.
当m<0时,有m2+2m+1=0,
解得:m=-1;
当0<m≤1时,有m2-6m+1=0,
解得:m=3-2$\sqrt{2}$或m=3+2$\sqrt{2}$(舍去);
当m>1时,有m2-6m+1=0,
解得:m=3+2$\sqrt{2}$或m=3-2$\sqrt{2}$(舍去).
∴m的值有3个,即符合要求的直线有3个.
故选C.
点评 本题考查了一次函数图象上点的坐标特征以及三角形的面积,根据一次函数图象上点的坐标特征找出点A、B的坐标是解题的关键.

练习册系列答案
相关题目
16.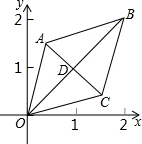 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°则第30秒时,菱形的对角线交点D的坐标为( )
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°则第30秒时,菱形的对角线交点D的坐标为( )
 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°则第30秒时,菱形的对角线交点D的坐标为( )
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°则第30秒时,菱形的对角线交点D的坐标为( )| A. | (1,-1) | B. | (-1,-1) | C. | ($\sqrt{2}$,0) | D. | (0,-$\sqrt{2}$) |
11.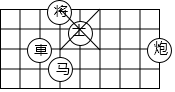 如图是棋盘的一部分,若用(1,3)表示
如图是棋盘的一部分,若用(1,3)表示 的位置,(2,2)表示
的位置,(2,2)表示 的位置,则
的位置,则 的位置可表示为( )
的位置可表示为( )
 如图是棋盘的一部分,若用(1,3)表示
如图是棋盘的一部分,若用(1,3)表示 的位置,(2,2)表示
的位置,(2,2)表示 的位置,则
的位置,则 的位置可表示为( )
的位置可表示为( )| A. | (1,6) | B. | (6,1) | C. | (6,0) | D. | (7,2) |
18.若方程mx+ny=6的两个解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,则m,n的值为( )
| A. | $\left\{\begin{array}{l}{m=4}\\{n=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=2}\\{n=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=-2}\\{n=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-4}\\{n=-2}\end{array}\right.$ |
15.计算$\sqrt{2}$×$\sqrt{8}$+$\root{3}{-27}$的结果为( )
| A. | ±1 | B. | 1 | C. | 4-3$\sqrt{3}$ | D. | 7 |
16.下列事件中,是确定性事件的是( )
| A. | 甲、乙、丙三人随意站成一排,而甲恰好站中间 | |
| B. | 从含有1个次品的10个产品中,随意抽取一个产品恰好是次品 | |
| C. | 早晨,太阳从西方升起 | |
| D. | 明天早晨八点是上班高峰期,学校门前的公路上必塞 |

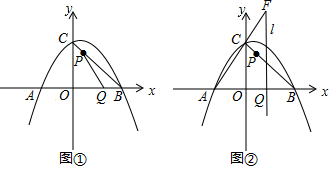
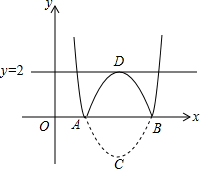 抛物线y=x2+bx+c与x轴交于点A、B,顶点为C,若将此抛物线沿x轴向上翻折,使点C落在点D处,得到如图所示图形记作图形F.
抛物线y=x2+bx+c与x轴交于点A、B,顶点为C,若将此抛物线沿x轴向上翻折,使点C落在点D处,得到如图所示图形记作图形F.